题目内容
13. 已知直三棱柱底面各边的比为17:10:9,侧棱长为16cm,全面积为1440cm2,求底面各边之长.(提示:设△ABC的三边长分别为a,b,c,记p=$\frac{1}{2}$(a+b+c),则△ABC的面积S△ABC=$\sqrt{p(p-a)(p-b)(p-c)}$.
已知直三棱柱底面各边的比为17:10:9,侧棱长为16cm,全面积为1440cm2,求底面各边之长.(提示:设△ABC的三边长分别为a,b,c,记p=$\frac{1}{2}$(a+b+c),则△ABC的面积S△ABC=$\sqrt{p(p-a)(p-b)(p-c)}$.
分析 设底面三边长分别为17x cm、10x cm、9x cm,由余弦定理求出长为17x的边所对的三角形内角的余弦值,从而求出直三棱柱的全面积为576x+72x2=1440,由此能求出底面各边之长.
解答 解:设底面三边长分别为17x cm、10x cm、9x cm,
S侧=(17x+10x+9x)•16=576x.
设长为17x的边所对的三角形内角为α,
则cosα=$\frac{(10x)^{2}+(9x)^{2}-(17x)^{2}}{2×10x×9x}$=-$\frac{3}{5}$,
∴sinα=$\sqrt{1-(-\frac{3}{5})^{2}}$=$\frac{4}{5}$.
∴S底=$\frac{1}{2}$•10x•9x•$\frac{4}{5}$=36x2.
∴576x+72x2=1440,解得x=2.
∴三边长分别为34 cm、20 cm、18 cm.
点评 本题考查直三棱柱底面各边长的求法,是中档题,解题时要注意余弦定理的合理运用.

练习册系列答案
相关题目
3.使|x-4|+|x-3|<a有实数解a的取值范围是( )
| A. | a>7 | B. | 1<a<7 | C. | a>1 | D. | a<7 |
8. 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
(1)求证:BF∥平面A1EC;
(2)求证:平面A1EC⊥平面ACC1A1.
(3)若各棱长相等,求二面角E-AC-B正切值.
 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.(1)求证:BF∥平面A1EC;
(2)求证:平面A1EC⊥平面ACC1A1.
(3)若各棱长相等,求二面角E-AC-B正切值.
3.函数f(x)=2(x-1)sinπx-1在区间[-2012,2014]内所有零点之和为( )
| A. | 2012 | B. | 4024 | C. | 2014 | D. | 4025 |
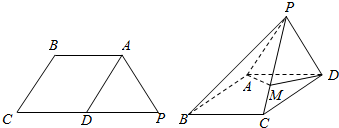 已知梯形ABCP,如图(1)所示,D是CP边的中点,AB∥PC,且2AB=PC,△APD为等边三角形,现将平面APD沿AD翻折,使平面APD⊥平面ABCD,得到如图(2)所示的四棱锥P-ABCD,点M在棱PC上,且PM=$\sqrt{3}$MC.
已知梯形ABCP,如图(1)所示,D是CP边的中点,AB∥PC,且2AB=PC,△APD为等边三角形,现将平面APD沿AD翻折,使平面APD⊥平面ABCD,得到如图(2)所示的四棱锥P-ABCD,点M在棱PC上,且PM=$\sqrt{3}$MC.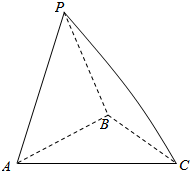 如图所示的三棱锥P-ABC的三条侧棱两两垂直,且PB=1,PA=$\sqrt{3}$,PC=$\sqrt{6}$.
如图所示的三棱锥P-ABC的三条侧棱两两垂直,且PB=1,PA=$\sqrt{3}$,PC=$\sqrt{6}$.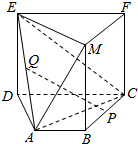 如图,矩形CDEF所在的平面与直角梯形ABCD所在的平面垂直,其中AB∥CD,AB=1,BC=$\frac{1}{2}CD=2$,BC⊥CD,MB∥FC,MB=FC=3.P、Q分别为BC、AE的中点.
如图,矩形CDEF所在的平面与直角梯形ABCD所在的平面垂直,其中AB∥CD,AB=1,BC=$\frac{1}{2}CD=2$,BC⊥CD,MB∥FC,MB=FC=3.P、Q分别为BC、AE的中点.