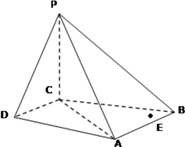题目内容
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.求证: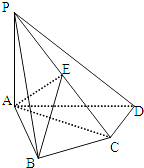
(Ⅰ)CD⊥AE;
(Ⅱ)PD⊥平面ABE.
【答案】证明:(Ⅰ)∵PA⊥底面ABCD,∴PA⊥CD,又AC⊥CD,PA∩AC=A,
故CD⊥平面PAC.
又AE平面PAC,∴CD⊥AE.
(Ⅱ)由题意:AB⊥AD,
∴AB⊥平面PAD,从而AB⊥PD.
又AB=BC,且∠ABC=60°,
∴AC=AB,从而AC=PA.
又E为PC之中点,∴AE⊥PC.
由(Ⅰ)知:AE⊥CD,∴AE⊥平面PCD,从而AE⊥PD.
又AB∩AE=A,
故PD⊥平面ABE

【解析】(1)根据题意结合已知条件利用线面垂直的性质定理得到线线垂直再结合线面垂直的判定定理即可得出结论。(2)利用已知的线面垂直得出线线垂直再结合(1)的结论由线面垂直的判定定理即可得证。

练习册系列答案
相关题目