题目内容
已知函数
(1)当x≤0时,函数f(x)在(-1,f(-1))处的切线方程为x-3y+1=0,求m的值;
(2)当x>0时,设f(x)+1的反函数为g-1(x)(g-1(x)的定义域即是f(x)+1的值域).证明:函数
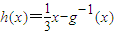 在区间(e,3)内无零点,在区间(3,e2)内有且只有一个零点;
在区间(e,3)内无零点,在区间(3,e2)内有且只有一个零点;(3)求函数f(x)的极值.
【答案】分析:(1)由题意得f'(-1)=1-2m所以函数f(x)在(-1,f(-1))处的切线方程为:(3-6m)x-3y+2-3m=0,又因为函数f(x)在(-1,f(-1))处的切线方程为x-3y+1=0所以解得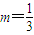 .
.
(2)当x>0时g-1(x)=lnx(x>1),所以 所以
所以 解得可知h(x)在(e,3)上为减函数,在(3,e2)上为增函数,在x=3处取得极小值.进而可以得到答案.
解得可知h(x)在(e,3)上为减函数,在(3,e2)上为增函数,在x=3处取得极小值.进而可以得到答案.
(3)当x>0时,f(x)=ex-1在(0,+∞)上单调递增,且f(x)=ex-1>0.当x≤0时,f'(x)=x2+2mx=x(x+2m).当m>0时,f'(x)=x2+2mx=x(x+2m),令f'(x)=0,得x1=-2m,x2=0.当x<-2m时,f'(x)>0当-2m<x<0时,f'(x)<0,f(x)在(-∞,-2m]上单调递增,在(-2m,0]上单调递减.有极值.
当m<0时f'(x)=x2+2mx=x(x+2m)>0,f(x)在R上是增函数,无极值
当m=0时f'(x)=x2≥0,f(x)在R上是增函数,无极值.
解答:解:(1)当x≤0时, ,
, f'(x)=x2+2mx,f'(-1)=1-2m
f'(x)=x2+2mx,f'(-1)=1-2m
函数f(x)在(-1,f(-1))处的切线方程为:
整理得:(3-6m)x-3y+2-3m=0
所以有 ,
,
解得 .
.
(2)当x>0时,f(x)+1=ex,
所以g-1(x)=lnx(x>1), =
= ,
,
令h'(x)>0得x>3;令h'(x)<0得1<x<3,令h'(x)=0得x=3,
故知函数h(x)在区间(1,3)上为减函数,在区间(3,+∞)为增函数,在x=3处取得极小值,
进而可知h(x)在(e,3)上为减函数,在(3,e2)上为增函数,在x=3处取得极小值.
又∵ .
.
所以,函数 在区间(e,3)内无零点,在区间(3,e2)有且只有一个零点
在区间(e,3)内无零点,在区间(3,e2)有且只有一个零点
(3)当x>0时,f(x)=ex-1在(0,+∞)上单调递增,且f(x)=ex-1>0.
当x≤0时,f'(x)=x2+2mx=x(x+2m)
①若m=0,f'(x)=x2≥0,则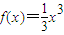 在(-∞,0]上单调递增,且
在(-∞,0]上单调递增,且 .
.
又f(0)=0,∴f(x)在R上是增函数,无极值.
②若m<0,f'(x)=x2+2mx=x(x+2m)>0,则 在(-∞,0]上单调递增.
在(-∞,0]上单调递增.
同理,f(x)在R上是增函数,无极值.
③若m>0,f'(x)=x2+2mx=x(x+2m),令f'(x)=0,得x1=-2m,x2=0.
当x<-2m时,f'(x)>0
当-2m<x<0时,f'(x)<0
所以, 在(-∞,-2m]上单调递增,在(-2m,0]上单调递减.
在(-∞,-2m]上单调递增,在(-2m,0]上单调递减.
又f(x)在(0,+∞)上单调递增,故[f(x)]极小=f(0)=0,
综上,当m>0时,[f(x)]极小=f(0)=0, .
.
当m≤0时,f(x)无极值.
点评:本题考查利用导数解决极值问题,关键要注意其中分类讨论是本题的难点,由于函数是分段函数所以在讨论时要细心仔细,很大方面考查了运算能力.
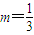 .
.(2)当x>0时g-1(x)=lnx(x>1),所以
 所以
所以 解得可知h(x)在(e,3)上为减函数,在(3,e2)上为增函数,在x=3处取得极小值.进而可以得到答案.
解得可知h(x)在(e,3)上为减函数,在(3,e2)上为增函数,在x=3处取得极小值.进而可以得到答案.(3)当x>0时,f(x)=ex-1在(0,+∞)上单调递增,且f(x)=ex-1>0.当x≤0时,f'(x)=x2+2mx=x(x+2m).当m>0时,f'(x)=x2+2mx=x(x+2m),令f'(x)=0,得x1=-2m,x2=0.当x<-2m时,f'(x)>0当-2m<x<0时,f'(x)<0,f(x)在(-∞,-2m]上单调递增,在(-2m,0]上单调递减.有极值.
当m<0时f'(x)=x2+2mx=x(x+2m)>0,f(x)在R上是增函数,无极值
当m=0时f'(x)=x2≥0,f(x)在R上是增函数,无极值.
解答:解:(1)当x≤0时,
 ,
, f'(x)=x2+2mx,f'(-1)=1-2m
f'(x)=x2+2mx,f'(-1)=1-2m函数f(x)在(-1,f(-1))处的切线方程为:

整理得:(3-6m)x-3y+2-3m=0
所以有
 ,
,解得
 .
.(2)当x>0时,f(x)+1=ex,
所以g-1(x)=lnx(x>1),
 =
= ,
,
令h'(x)>0得x>3;令h'(x)<0得1<x<3,令h'(x)=0得x=3,
故知函数h(x)在区间(1,3)上为减函数,在区间(3,+∞)为增函数,在x=3处取得极小值,
进而可知h(x)在(e,3)上为减函数,在(3,e2)上为增函数,在x=3处取得极小值.
又∵
 .
.所以,函数
 在区间(e,3)内无零点,在区间(3,e2)有且只有一个零点
在区间(e,3)内无零点,在区间(3,e2)有且只有一个零点(3)当x>0时,f(x)=ex-1在(0,+∞)上单调递增,且f(x)=ex-1>0.
当x≤0时,f'(x)=x2+2mx=x(x+2m)
①若m=0,f'(x)=x2≥0,则
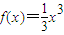 在(-∞,0]上单调递增,且
在(-∞,0]上单调递增,且 .
.又f(0)=0,∴f(x)在R上是增函数,无极值.
②若m<0,f'(x)=x2+2mx=x(x+2m)>0,则
 在(-∞,0]上单调递增.
在(-∞,0]上单调递增.同理,f(x)在R上是增函数,无极值.
③若m>0,f'(x)=x2+2mx=x(x+2m),令f'(x)=0,得x1=-2m,x2=0.
当x<-2m时,f'(x)>0
当-2m<x<0时,f'(x)<0
所以,
 在(-∞,-2m]上单调递增,在(-2m,0]上单调递减.
在(-∞,-2m]上单调递增,在(-2m,0]上单调递减.又f(x)在(0,+∞)上单调递增,故[f(x)]极小=f(0)=0,

综上,当m>0时,[f(x)]极小=f(0)=0,
 .
.当m≤0时,f(x)无极值.
点评:本题考查利用导数解决极值问题,关键要注意其中分类讨论是本题的难点,由于函数是分段函数所以在讨论时要细心仔细,很大方面考查了运算能力.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

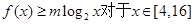 恒成立,求m的取值范围
恒成立,求m的取值范围
 恒成立,求m的取值范围.
恒成立,求m的取值范围.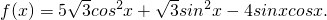
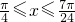 ,求f(x)的单调区间.
,求f(x)的单调区间.
 ,求f(x)的单调区间.
,求f(x)的单调区间.