Question

16．已知函数f（x）=$\sqrt{9-x^2}+\frac{1}{{\sqrt{x+2}}}$的定义域为集合A，B={x|x＜a}．
（1）若A⊆B，求a的取值范围；
（2）若全集U={x|x≤4}，a=-1，求∁_UA及A∩（∁_UB）．

Answer 1

分析 （1）首先求出集合A，根据A⊆B，利用子集的概念，考虑集合端点值列式求得a的范围；
（2）直接运用补集及交集的概念进行求解．

解答 解：（1）要使函数f（x）=$\sqrt{9-x^2}+\frac{1}{{\sqrt{x+2}}}$有意义，则$\left\{\begin{array}{l}{9-{x}^{2}≥0}\\{x+2＞0}\end{array}\right.$，解得：-2＜x≤3．
所以，A={x|-2＜x≤3}．
又因为B={x|x＜a}，要使A⊆B，则a＞3．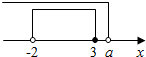

（2）因为U={x|x≤4}，A={x|-2＜x≤3}，所以C_UA={x|x≤-2或3＜x≤4}．
又因为a=-1，所以B={x|x＜-1}．
所以C_UB={-1≤x≤4}，所以，A∩（C_UB）=A={x|-2＜x≤3}∩{-1≤x≤4}={x|-1≤x≤3}．

点评 本题考查了函数的定义域及其求法，考查了交集和补集的混合运算，求解集合的运算时，利用数轴分析能起到事半功倍的效果，此题是基础题．