题目内容
如图,已知两圆C1 :(x-4 )2+y2=169 ,C2 :(x+4 )2+y2 =9 ,动圆在圆C1 内部且和圆C1 相内切,和圆C2 相外切,求动圆圆心的轨迹方程
.

解:设动圆圆心M(x ,y) ,半径为r ,
由题意动圆M 内切于圆C1 ,圆M 外切于圆C2 ,
∴|MC1|=13-r, |MC2|=3+r,
∴|MC1|+|MC2|=16 ,
∴动圆圆心M 的轨迹是以C1 、C2 为焦点的椭圆,
且2a=16 ,2c=8 , b2=a2-c2=64-16=48 .
故所求动圆圆心的轨迹方程为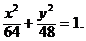
由题意动圆M 内切于圆C1 ,圆M 外切于圆C2 ,
∴|MC1|=13-r, |MC2|=3+r,
∴|MC1|+|MC2|=16 ,
∴动圆圆心M 的轨迹是以C1 、C2 为焦点的椭圆,
且2a=16 ,2c=8 , b2=a2-c2=64-16=48 .
故所求动圆圆心的轨迹方程为
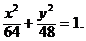

练习册系列答案
相关题目
 如图,已知双曲线C1:
如图,已知双曲线C1: (考生注意:请在下面两题中任选一题作答,如果都做,则按所做第1题评分)
(考生注意:请在下面两题中任选一题作答,如果都做,则按所做第1题评分) (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: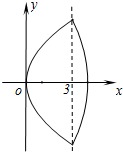 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: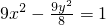 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;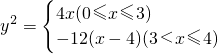 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值; 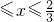 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: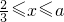 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.