题目内容
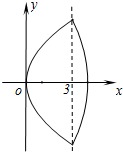 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: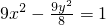 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.
(2)如图,已知“盾圆D”的方程为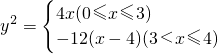 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
(3)由抛物线弧E1:y2=4x(0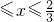 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: (
(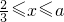 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.
(1)解:由△MF1F2的周长为6得2(a+c)=6,即a+c=3,
椭圆C1与双曲线C2: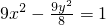 有相同的焦点,所以c=1,所以a=2,b2=a2-c2=3,
有相同的焦点,所以c=1,所以a=2,b2=a2-c2=3,
椭圆C1的方程为 ;
;
(2)证明:设“盾圆D”上的任意一点M的坐标为(x,y),d2=|x-3|.
当M∈C1时,y2=4x(0≤x≤3), =|x+1|,
=|x+1|,
则d1+d2=|x+1|+|x-3|=(x+1)+(3-x)=4;
当M∈C2时,y2=-12(x-4)(3<x≤4), =|7-x|,
=|7-x|,
则d1+d2=|7-x|+|x-3|=(7-x)+(x-3)=4;
所以d1+d2=4为定值;
(3)显然“盾圆E”由两部分合成,所以按A在抛物线弧E1或椭圆弧E2上加以分类,由“盾圆E”的对称性,不妨设A在x轴上方(或x轴上):
当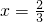 时,
时,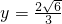 ,此时r=
,此时r= ,cosα=-
,cosα=- ;
;
当- ≤cosα≤1时,A在椭圆弧E2上,
≤cosα≤1时,A在椭圆弧E2上,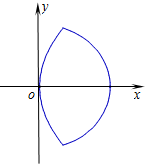
由题设知A(1+r1cosα,r1sinα)代入 得,3(1+r1cosα)2+4
得,3(1+r1cosα)2+4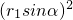 -12=0,
-12=0,
整理得(4-cos2α)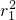 +6r1cosα-9=0,
+6r1cosα-9=0,
解得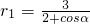 或
或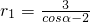 (舍去).
(舍去).
当-1≤cosα≤- 时A在抛物线弧E1上,
时A在抛物线弧E1上,
由方程或定义均可得到r1=2+r1cosα,于是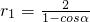 ,
,
综上,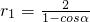 (-1
(-1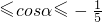 )或
)或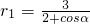 (-
(- ≤cosα≤1);
≤cosα≤1);
相应地,B(1-r2cosα,-r2sinα),
当-1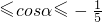 时A在抛物线弧E1上,B在椭圆弧E2上,
时A在抛物线弧E1上,B在椭圆弧E2上,
 =
=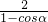
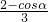 =
=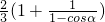 ∈[1,
∈[1, ];
];
当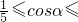 1时A在椭圆弧E2上,B在抛物线弧E1上,
1时A在椭圆弧E2上,B在抛物线弧E1上,
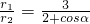 •
•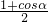 =
= ∈[
∈[ ,1];
,1];
当-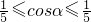 时A、B在椭圆弧E2上,
时A、B在椭圆弧E2上,
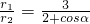
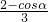 =
=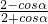 ∈(
∈( ,
, );
);
综上 的取值范围是[
的取值范围是[ ,
, ].
].
分析:(1)由△MF1F2的周长为6得a+c=3,由椭圆与双曲线共焦点可得c值,据平方关系可求得b;
(2)设“盾圆D”上的任意一点M的坐标为(x,y),d2=|x-3|.分M∈C1时,M∈C2时两种情况表示出d1,再分别计算d1+d2即可求得定值;
(3)由“盾圆E”的对称性,不妨设A在x轴上方(或x轴上),当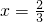 时,
时,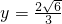 ,此时r=
,此时r= ,cosα=-
,cosα=- ,分类讨论:-
,分类讨论:- ≤cosα≤1时,A在椭圆弧E2上,-1≤cosα≤-
≤cosα≤1时,A在椭圆弧E2上,-1≤cosα≤- 时A在抛物线弧E1上,由条件可表示出此时r1,相应地,B(1-r2cosα,-r2sinα),再按-1
时A在抛物线弧E1上,由条件可表示出此时r1,相应地,B(1-r2cosα,-r2sinα),再按-1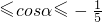 时A在抛物线弧E1上,B在椭圆弧E2上,当
时A在抛物线弧E1上,B在椭圆弧E2上,当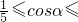 1时A在椭圆弧E2上,B在抛物线弧E1上,
1时A在椭圆弧E2上,B在抛物线弧E1上,
当-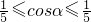 时A、B在椭圆弧E2上,利用三角函数性质分别求出
时A、B在椭圆弧E2上,利用三角函数性质分别求出 的范围即可.
的范围即可.
点评:本题考查直线与圆锥曲线的位置关系、两点间距离公式及椭圆方程的求解,考查学生综合运用所学知识分析问题解决问题的能力,本题综合性强,难度大,对能力要求高.
椭圆C1与双曲线C2:
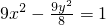 有相同的焦点,所以c=1,所以a=2,b2=a2-c2=3,
有相同的焦点,所以c=1,所以a=2,b2=a2-c2=3,椭圆C1的方程为
 ;
;(2)证明:设“盾圆D”上的任意一点M的坐标为(x,y),d2=|x-3|.
当M∈C1时,y2=4x(0≤x≤3),
 =|x+1|,
=|x+1|,则d1+d2=|x+1|+|x-3|=(x+1)+(3-x)=4;
当M∈C2时,y2=-12(x-4)(3<x≤4),
 =|7-x|,
=|7-x|,则d1+d2=|7-x|+|x-3|=(7-x)+(x-3)=4;
所以d1+d2=4为定值;
(3)显然“盾圆E”由两部分合成,所以按A在抛物线弧E1或椭圆弧E2上加以分类,由“盾圆E”的对称性,不妨设A在x轴上方(或x轴上):
当
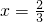 时,
时,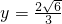 ,此时r=
,此时r= ,cosα=-
,cosα=- ;
;当-
 ≤cosα≤1时,A在椭圆弧E2上,
≤cosα≤1时,A在椭圆弧E2上,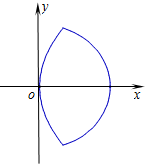
由题设知A(1+r1cosα,r1sinα)代入
 得,3(1+r1cosα)2+4
得,3(1+r1cosα)2+4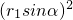 -12=0,
-12=0,整理得(4-cos2α)
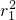 +6r1cosα-9=0,
+6r1cosα-9=0,解得
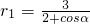 或
或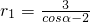 (舍去).
(舍去).当-1≤cosα≤-
 时A在抛物线弧E1上,
时A在抛物线弧E1上,由方程或定义均可得到r1=2+r1cosα,于是
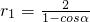 ,
,综上,
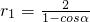 (-1
(-1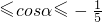 )或
)或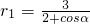 (-
(- ≤cosα≤1);
≤cosα≤1);相应地,B(1-r2cosα,-r2sinα),
当-1
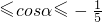 时A在抛物线弧E1上,B在椭圆弧E2上,
时A在抛物线弧E1上,B在椭圆弧E2上, =
=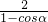
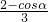 =
=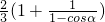 ∈[1,
∈[1, ];
];当
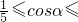 1时A在椭圆弧E2上,B在抛物线弧E1上,
1时A在椭圆弧E2上,B在抛物线弧E1上,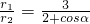 •
•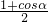 =
= ∈[
∈[ ,1];
,1];当-
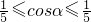 时A、B在椭圆弧E2上,
时A、B在椭圆弧E2上,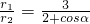
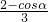 =
=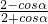 ∈(
∈( ,
, );
);综上
 的取值范围是[
的取值范围是[ ,
, ].
].分析:(1)由△MF1F2的周长为6得a+c=3,由椭圆与双曲线共焦点可得c值,据平方关系可求得b;
(2)设“盾圆D”上的任意一点M的坐标为(x,y),d2=|x-3|.分M∈C1时,M∈C2时两种情况表示出d1,再分别计算d1+d2即可求得定值;
(3)由“盾圆E”的对称性,不妨设A在x轴上方(或x轴上),当
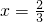 时,
时,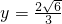 ,此时r=
,此时r= ,cosα=-
,cosα=- ,分类讨论:-
,分类讨论:- ≤cosα≤1时,A在椭圆弧E2上,-1≤cosα≤-
≤cosα≤1时,A在椭圆弧E2上,-1≤cosα≤- 时A在抛物线弧E1上,由条件可表示出此时r1,相应地,B(1-r2cosα,-r2sinα),再按-1
时A在抛物线弧E1上,由条件可表示出此时r1,相应地,B(1-r2cosα,-r2sinα),再按-1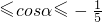 时A在抛物线弧E1上,B在椭圆弧E2上,当
时A在抛物线弧E1上,B在椭圆弧E2上,当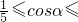 1时A在椭圆弧E2上,B在抛物线弧E1上,
1时A在椭圆弧E2上,B在抛物线弧E1上,当-
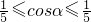 时A、B在椭圆弧E2上,利用三角函数性质分别求出
时A、B在椭圆弧E2上,利用三角函数性质分别求出 的范围即可.
的范围即可.点评:本题考查直线与圆锥曲线的位置关系、两点间距离公式及椭圆方程的求解,考查学生综合运用所学知识分析问题解决问题的能力,本题综合性强,难度大,对能力要求高.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: