题目内容
 (考生注意:请在下面两题中任选一题作答,如果都做,则按所做第1题评分)
(考生注意:请在下面两题中任选一题作答,如果都做,则按所做第1题评分)(1)(坐标系与参数方程选做题)
曲线C1:
|
|
1
1
.(2)(几何证明选讲选做题)
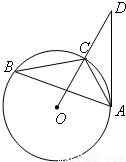
如图,已知:△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠B=30°,AC=1,则AD的长为
| 3 |
| 3 |
分析:(1)把曲线C1和曲线C2的方程化为普通方程,求出圆心到直线的距离,将此距离减去半径,即得所求.
(2)根据同弧所对的圆周角和圆心角之间的关系,得到∠AOC=60°,根据含有60°角的等腰三角形是一个等边三角形,可得△AOC是等边三角形,从而得到OA=AC=1,利用勾股定理求得AD的长.
(2)根据同弧所对的圆周角和圆心角之间的关系,得到∠AOC=60°,根据含有60°角的等腰三角形是一个等边三角形,可得△AOC是等边三角形,从而得到OA=AC=1,利用勾股定理求得AD的长.
解答:解:(1)曲线C1:
(θ为参数)消去参数,化为普通方程为 (x-1)2+y2=1,表示以(1,0)为圆心,以1为半径的圆.
曲线C2:
(t为参数)即 x+y+2
-1,表示一条直线.
圆心到直线的距离等于
=2,故曲线C1:上的点到到曲线C2的距离最小值等于2-1=1,
故答案为 1.
(2):∵∠B=30,∠AOC与∠B同时对应着弧AC,∴∠AOC=60°.
∵OA=OC,∴△AOC是等边三角形,∴OA=AC=1,
∵∠OAD=90°,∠D=30°,AD=
AO=
,
故答案为
.
|
曲线C2:
|
| 2 |
圆心到直线的距离等于
|1+0+2
| ||
|

故答案为 1.
(2):∵∠B=30,∠AOC与∠B同时对应着弧AC,∴∠AOC=60°.
∵OA=OC,∴△AOC是等边三角形,∴OA=AC=1,
∵∠OAD=90°,∠D=30°,AD=
| 3 |
| 3 |
故答案为
| 3 |
点评:本题考查把参数方程化为普通方程的方法,点到直线的距离公式的应用,直线和圆的位置关系的应用.以及和圆有关的比例线段,考查同弧所对的圆周角等于圆心角的一半,
本题解题的关键是应用含有30°角的直角三角形的性质做出有关的数据,是一个基础题.
本题解题的关键是应用含有30°角的直角三角形的性质做出有关的数据,是一个基础题.

练习册系列答案
相关题目
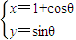 (θ为参数)上的点到曲线C2:
(θ为参数)上的点到曲线C2: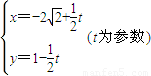 上的点的最短距离为 .
上的点的最短距离为 .