题目内容
(本小题满分12分)为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.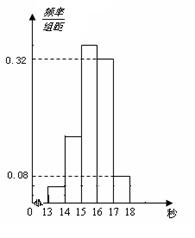
⑴将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
⑵求调查中随机抽取了多少个学生的百米成绩;
⑶若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
(1)估计该年段学生中百米成绩在[16,17)内的人数为320人。
(2)调查中随机抽取了50个学生的百米成绩. (3)P(A )= 。
。
解析试题分析:(1)根据频率分步直方图中小正方形的面积是这组数据的频率,用长乘以宽得到面积,即为频率.
(II)根据所有的频率之和是1,列出关于x的方程,解出x的值做出样本容量的值,即调查中随机抽取了50个学生的百米成绩.
(III)本题是一个古典概型,试验发生所包含的事件是从第一、五组中随机取出两个成绩,满足条件的事件是成绩的差的绝对值大于1秒,列举出事件数,根据古典概型概率公式得到结果.
解:(1)百米成绩在[16,17)内的频率为0.32 1="0.32." 0.32
1="0.32." 0.32 1000=320
1000=320
∴估计该年段学生中百米成绩在[16,17)内的人数为320人。 ……2分
(2)设图中从左到右前3个组的频率分别为3x,8x ,19x 依题意,得 3x+8x+19x+0.32 1+0.08
1+0.08 1="1" ,∴x=0.02 ……4分
1="1" ,∴x=0.02 ……4分
设调查中随机抽取了n 个学生的百米成绩,则 ∴n=50
∴n=50
∴调查中随机抽取了50个学生的百米成绩. ……6分
(3)百米成绩在第一组的学生数有3 0.02
0.02 1
1 50=3,记他们的成绩为a,b,c
50=3,记他们的成绩为a,b,c
百米成绩在第五组的学生数有0.08 1
1 50= 4,记他们的成绩为m,n,p,q
50= 4,记他们的成绩为m,n,p,q
则从第一、五组中随机取出两个成绩包含的基本事件有
{a,b},{a,c},{a,m},{a,n},{a,p},{a,q},{b,c},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},
{c,p},{c,q},{m,n},{m,p},{m,q},{n,p},{n,q},{p,q},共21个 ……9分
设事件A为满足成绩的差的绝对值大于1秒,则事件A所包含的基本事件有{a,m},{a,n},{a,p},{a,q},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},共12个,……10分
所以P(A )= ……12分
……12分
考点:本试题主要考查了样本估计总体,考查古典概型的概率公式,考查频率分布直方图等知识,考查数据处理能力和分析问题、解决问题的能力。
点评:解决该试题的关键是利用直方图得到各个区间的概率值,进而结合古典概型概率公式,确定基本事件空间,和事件A发生的基本事件数,进而得到结论。

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案(本题满分12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
| | 文艺节目 | 新闻节目 | 总计 |
| 20至40岁 | 40 | 10 | 50 |
| 大于40岁 | 20 | 30 | 50 |
| 总计 | 60 | 40 | 100 |
(2)20至40岁,大于40岁中各抽取1名观众,求两人恰好都收看文艺节目的概率.
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量( 吨)与相应的生产能耗
吨)与相应的生产能耗 (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
 | 3 | 4 | 5 | 6 |
 | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出
 关于
关于 的线性回归方程
的线性回归方程 ;
;(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式
 ,
, )
) (本小题满分13分)
某种产品的广告费支出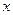 与销售额
与销售额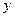 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
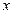 | 2 | 4 | 5 | 6 | 8 |
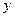 | 30 | 40 | 60 | 50 | 70 |
(Ⅰ)求回归直线方程;
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(Ⅲ)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的
绝对值不超过5的概率。
(参考数据:
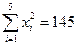
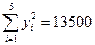
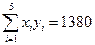 ,
,参考公式:回归直线方程
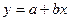 ,其中
,其中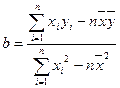 )
) 
 的分布列及其数学期望。
的分布列及其数学期望。 某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .若备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .若备选的5个居民小区中有三个非低碳小区,两个低碳小区.
 ,调查显示其“低碳族”的比例为1:2,数据如图1所示,经过大力宣传,三个月后又进行一次调查,数据如图2所示,问这时小区
,调查显示其“低碳族”的比例为1:2,数据如图1所示,经过大力宣传,三个月后又进行一次调查,数据如图2所示,问这时小区
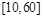 间的频率是多少?
间的频率是多少?
