题目内容
如图,在斜三棱柱ABC-A1B1C1中,∠A1AB=∠A1AC,AB=AC,侧面B1BCC1与底面ABC所成的二面角为120°,E、F分别是棱CB1、AA1的中点.
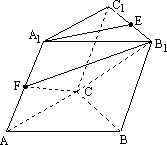
(1)AA1求与底面ABC所成的角;
(2)证明EA1∥平面B1FC;
答案:
解析:
解析:
|
(1)解:过A1作平面A1H⊥平面ABC,垂足为H.连接AH,并延长BC交于G,连接EG,于是∠A1AH为A1A与底面ABC所成的角. 因为∠A1AB=∠A1AC,所以AG为的∠BAC平分线 又因为AB=AC,所以AG⊥BC,且G为BC的中点 因此,由三垂线定理A1A⊥BC 因为A1A∥B1B,且EG∥B1B,所以EG⊥BC,于是为∠AGE二面角A-BC-E的平面角,即∠AGE=120°,由于四边形A1AGE为平行四边形,得∠A1AG=60° 所以,A1A与底面ABC所成的角度为60° (II)证明:设EG与B1C的交点为P,则点P为EG的中点,连结PF. 在平行四边形AGEA1中,因为F是A1A的中点,∴A1F∥EP且A1F=EP∴A1FPE为平行四边形∴A1E∥FP,而FP |

练习册系列答案
相关题目
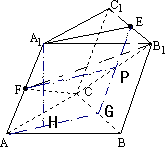
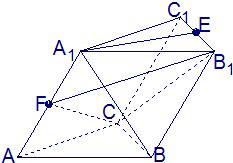 如图,在斜三棱柱ABC-A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120°,E、F分别是棱B1C1、A1A的中点
如图,在斜三棱柱ABC-A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120°,E、F分别是棱B1C1、A1A的中点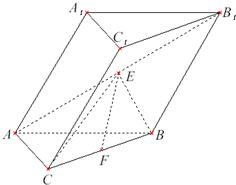 如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.  如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,又BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H一定在( )
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,又BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H一定在( )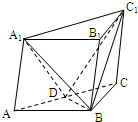 (2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点.
(2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点. (2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=
(2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=