题目内容
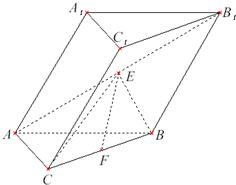 如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点. (1)求证:直线EF∥平面A1ACC1;
(2)在线段AB上确定一点G,使平面EFG⊥平面ABC,并给出证明;
(3)记三棱锥A-BCE的体积为V,且V∈[
| 3 | 2 |
分析:(1)连接A1C,A1E,结合菱形的性质及F是BC的中点,由三角形的中位线定理,可证得EF∥A1C,由线面平行的判定定理即可得到直线EF∥平面A1ACC1;
(2)取G为线段AB上靠近B点的四等分点,连接EG,FG,由菱形的性质及E是A1B的中点,可得EG⊥AB,又由平面A1ABB1⊥平面ABC,根据面面垂直的性质定理可得EG⊥平面ABC,又由面面垂直的判定定理,即可得到平面EFG⊥平面ABC;
(3)由△A1AB是边长为a的等边三角形,则我们可以求出EG的长,结合(2)中EG⊥平面ABC,利用等体积法,我们易将棱锥A-BCE的体积为V表示为a表达式,结合V∈[
,12],构造关于a的不等式,解不等式即可得到答案.
(2)取G为线段AB上靠近B点的四等分点,连接EG,FG,由菱形的性质及E是A1B的中点,可得EG⊥AB,又由平面A1ABB1⊥平面ABC,根据面面垂直的性质定理可得EG⊥平面ABC,又由面面垂直的判定定理,即可得到平面EFG⊥平面ABC;
(3)由△A1AB是边长为a的等边三角形,则我们可以求出EG的长,结合(2)中EG⊥平面ABC,利用等体积法,我们易将棱锥A-BCE的体积为V表示为a表达式,结合V∈[
| 3 |
| 2 |
解答:(1)证明:连接A1C,A1E.因为 侧面A1ABB1是菱形,E是AB1的中点,所以 E也是A1B的中点,
又因为 F是BC的中点,所以 EF∥A1C.
因为 A1C?平面A1ACC1,EF?平面A1ACC1,所以 直线EF∥平面A1ACC1. …(4分)
(2)解:当
=
时,平面EFG⊥平面ABC,证明如下:…(5分)
连接EG,FG.因为 侧面A1ABB1是菱形,且∠A1AB=60°,所以△A1AB是等边三角形.
因为 E是A1B的中点,
=
,所以 EG⊥AB.
因为 平面A1ABB1⊥平面ABC,且平面A1ABB1∩平面ABC=AB,所以 EG⊥平面ABC.
又因为 EG?平面EFG,所以 平面EFG⊥平面ABC. …(8分)
(3)解:因为△A1AB是边长为a的等边三角形,所以 EG=
a,
所以 V=VA-BCE=VE-ABC=
•
AC•BC•EG=
a3.
根据
≤
a3≤12,解得2
≤a≤4
,即 a∈[2
,4
]. …(12分)
又因为 F是BC的中点,所以 EF∥A1C.
因为 A1C?平面A1ACC1,EF?平面A1ACC1,所以 直线EF∥平面A1ACC1. …(4分)
(2)解:当
| BG |
| GA |
| 1 |
| 3 |
连接EG,FG.因为 侧面A1ABB1是菱形,且∠A1AB=60°,所以△A1AB是等边三角形.
因为 E是A1B的中点,
| BG |
| GA |
| 1 |
| 3 |
因为 平面A1ABB1⊥平面ABC,且平面A1ABB1∩平面ABC=AB,所以 EG⊥平面ABC.
又因为 EG?平面EFG,所以 平面EFG⊥平面ABC. …(8分)
(3)解:因为△A1AB是边长为a的等边三角形,所以 EG=
| ||
| 4 |
所以 V=VA-BCE=VE-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 48 |
根据
| 3 |
| 2 |
| ||
| 48 |
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,平面与平面垂直的判定,其中(1)的关键是证得EF∥A1C,(2)的关键是证得EG⊥平面ABC,(3)的关键是将棱锥A-BCE的体积为V表示为a表达式,结合V∈[
,12],构造关于a的不等式.
| 3 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
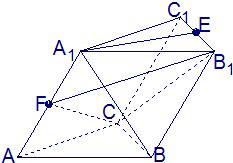 如图,在斜三棱柱ABC-A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120°,E、F分别是棱B1C1、A1A的中点
如图,在斜三棱柱ABC-A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120°,E、F分别是棱B1C1、A1A的中点 如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,又BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H一定在( )
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,又BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H一定在( )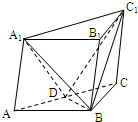 (2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点.
(2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点. (2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=
(2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=