题目内容
(16分)已知函数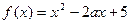
（
）.
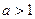(I)若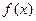
的定义域和值域均是
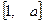，求实数
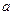的值；
(II)若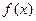在区间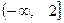
上是减函数，且对任意的
，
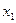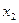
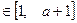，总有
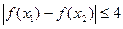，求实数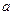的取值范围.
(Ⅰ)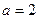 
.
(II)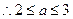 
.
解析
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
课课练江苏系列答案名牌中学课时作业系列答案明天教育课时特训系列答案浙江新课程三维目标测评课时特训系列答案题目内容
(16分)已知函数（）.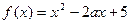
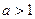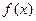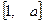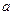(I)若的定义域和值域均是，求实数的值；
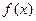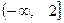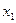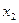
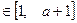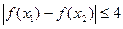(II)若在区间上是减函数，且对任意的，，总有，求实数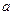的取值范围.
(Ⅰ) .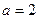
(II) .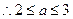
解析
课课练江苏系列答案名牌中学课时作业系列答案明天教育课时特训系列答案浙江新课程三维目标测评课时特训系列答案
，其中
，
，
.（1）若
，且
的最大值为2，最小值为
，求
的最小值；（2）若对任意实数
，不等式
，且存在
使得
成立，求
的值.
（
）．
的值域；
．
,函数
.
满足
,函数
是否具有奇偶性？如果有,求出相应的
判断函数
，
，且
，求函数
的对称轴或对称中心.
满足满足
；
，求
的最大值.
，在
处的
．
的解析式；
，若对任意
，总存在
，使得
成立，求实数
的取值范围．