题目内容
若实数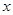 、
、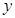 、
、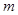 满足
满足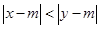 ,则称
,则称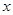 比
比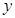 接近
接近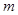 .
.
(1)若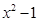 比3接近0,求
比3接近0,求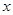 的取值范围;
的取值范围;
(2)对任意两个不相等的正数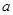 、
、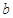 ,证明:
,证明: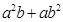 比
比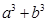 接近
接近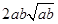 ;
;
(3)已知函数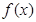 的定义域
的定义域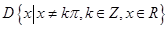 .任取
.任取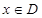 ,
,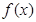 等于
等于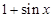 和
和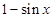 中接近0的那个值.写出函数
中接近0的那个值.写出函数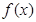 的解析式及最小值(结论不要求证明)
的解析式及最小值(结论不要求证明)
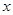 、
、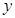 、
、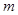 满足
满足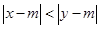 ,则称
,则称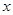 比
比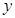 接近
接近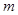 .
.(1)若
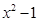 比3接近0,求
比3接近0,求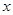 的取值范围;
的取值范围;(2)对任意两个不相等的正数
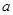 、
、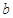 ,证明:
,证明: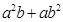 比
比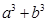 接近
接近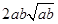 ;
;(3)已知函数
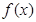 的定义域
的定义域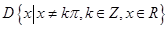 .任取
.任取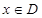 ,
,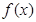 等于
等于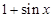 和
和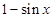 中接近0的那个值.写出函数
中接近0的那个值.写出函数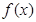 的解析式及最小值(结论不要求证明)
的解析式及最小值(结论不要求证明) (1) xÎ(-2,2);(2) a2b+ab2比a3+b3接近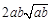 ; (3) f(x)的最小值为0。
; (3) f(x)的最小值为0。
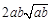 ; (3) f(x)的最小值为0。
; (3) f(x)的最小值为0。试题分析:(1)根据新定义得到不等式|x2-1|<3,然后求出x的范围即可.
(2)对任意两个不相等的正数a、b,依据新定义写出不等式,利用作差法证明:a2b+ab2比a3+b3接近2ab
 ,
,(3)依据新定义写出函数f(x)的解析式,f(x)= 1+sinx,x

1-sinx,x
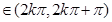
=1-|sinx|,x≠kπ直接写出它的奇偶性、最小正周期、最小值和单调性,即可.
(1) xÎ(-2,2); ---------------4分
(2) 对任意两个不相等的正数a、b,有
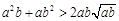 ,
,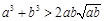 ,
, 因为
 ,
, 所以
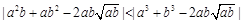 ,即a2b+ab2比a3+b3接近
,即a2b+ab2比a3+b3接近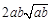 ; ------8分 (3)
; ------8分 (3) 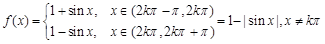 ,kÎZ,
,kÎZ, f(x)的最小值为0, --------------------12分
点评:解决该试题的关键是利用定义来表示出函数f(x)然后结合三角函数的性质来得到结论。

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
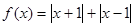 ,不等式
,不等式 的解集为
的解集为
 时,证明:
时,证明:
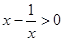 成立的充分不必要条件是( )
成立的充分不必要条件是( )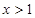

 或
或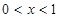
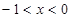 或
或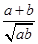 ≥2;③x2+
≥2;③x2+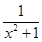 ≥1.其中正确的个数是( )
≥1.其中正确的个数是( )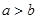 成立的必要而不充分的条件是( )
成立的必要而不充分的条件是( )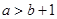
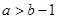
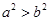
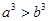
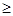 2x
2x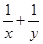 的最小值及对应的x、y值.
的最小值及对应的x、y值.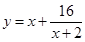 的最小值;
的最小值;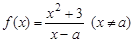 ,其中
,其中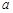 为非零常数.
为非零常数.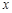 的不等式
的不等式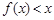 ;
; (Ⅱ)若当
(Ⅱ)若当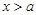 时,函数
时,函数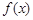 的最小值为3,求实数
的最小值为3,求实数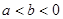 ,则有( )
,则有( ) 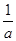 <
<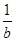
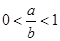
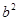 >
>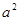
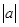 >
>