题目内容
已知曲线y=
和y=x2
(1)求它们的交点;
(2)分别求它们在交点处的切线方程;
(3)求两条切线与x轴所围成的三角形面积.
| 1 | x |
(1)求它们的交点;
(2)分别求它们在交点处的切线方程;
(3)求两条切线与x轴所围成的三角形面积.
分析:(1)联立方程可得曲线y=
和y=x2在它们的交点坐标;
(2)求导数,确定函数在(1,1)处的切线的斜率,从而可求切线方程;
(3)确定两条切线与x轴所围成的三角形三个顶点的坐标,即可求得两条切线与x轴所围成的三角形面积.
| 1 |
| x |
(2)求导数,确定函数在(1,1)处的切线的斜率,从而可求切线方程;
(3)确定两条切线与x轴所围成的三角形三个顶点的坐标,即可求得两条切线与x轴所围成的三角形面积.
解答: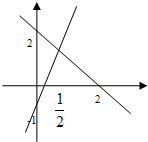 解:(1)联立方程可得
解:(1)联立方程可得
,解得x=1,y=1
∴曲线y=
和y=x2在它们的交点坐标是(1,1);…(2分)
(2)y=
的导函数为y′=-
,∴在(1,1)处的切线的斜率为-1,
∴切线方程为y-1=-(x-1),即y=-x+2
y=x2的导函数为y=2x,∴在(1,1)处的切线的斜率为2,
∴切线方程为y-1=2(x-1),即y=2x-1,…(8分)
(3)两条切线与x轴所围成的三角形如图所示,两条切线与x轴的交点坐标分别为(2,0),(
,0),两条切线交点是(1,1),
∴两条切线与x轴所围成的三角形面积是
.…(14分)
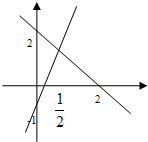 解:(1)联立方程可得
解:(1)联立方程可得
|
∴曲线y=
| 1 |
| x |
(2)y=
| 1 |
| x |
| 1 |
| x2 |
∴切线方程为y-1=-(x-1),即y=-x+2
y=x2的导函数为y=2x,∴在(1,1)处的切线的斜率为2,
∴切线方程为y-1=2(x-1),即y=2x-1,…(8分)
(3)两条切线与x轴所围成的三角形如图所示,两条切线与x轴的交点坐标分别为(2,0),(
| 1 |
| 2 |
∴两条切线与x轴所围成的三角形面积是
| 3 |
| 4 |
点评:本题考查曲线的切线方程,考查三角形面积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 如图,已知曲线
如图,已知曲线
 如图,已知曲线C:
如图,已知曲线C: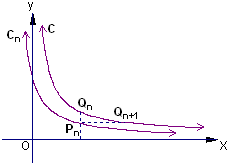 如图,已知曲线C:
如图,已知曲线C: