题目内容
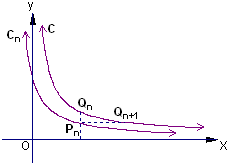如图，已知曲线C：y=| 1 |
| x |
| 1 |
| x+2-n |
（1）求点Q1、Q2的坐标；
（2）求数列{an} 的通项公式；
（3）记数列{an•yn+1} 的前n项和为Sn，求证sn＜
| 1 |
| 3 |
分析：（1）由Qn（xn，yn），Qn+1（xn+1，yn+1），知点Pn的坐标为（xn，yn+1），由此能求出点Q1、Q2的坐标．
（2）由Qn，Qn+1在曲线C上，知yn=
，yn+1=
，由Pn在曲线Cn上，知yn+1=
，由此能求出数列{an} 的通项公式．
（3）由xn=（xn-xn-1）+（xn-1-xn-2）+…+（x2-x1）+x1=2-（n-1）+2-（n-2）+…+2-1+1=1-
=2-21-n，知an•bn=（xn+1-xn）•（yn-yn+1）=2-n(
-
)=
(
-
)=
，由此入手能够证明sn＜
．
（2）由Qn，Qn+1在曲线C上，知yn=
| 1 |
| xn |
| 1 |
| xn+1 |
| 1 |
| xn+2-n |
（3）由xn=（xn-xn-1）+（xn-1-xn-2）+…+（x2-x1）+x1=2-（n-1）+2-（n-2）+…+2-1+1=1-
1-(
| ||
1-
|
| 1 |
| xn |
| 1 |
| xn+1 |
| 1 |
| 2n |
| 1 |
| 2-21-n |
| 1 |
| 2-2-n |
| 1 |
| (2•2n-2)• (2•2n-1) |
| 1 |
| 3 |
解答：解：（1）∵Qn（xn，yn），Qn+1（xn+1，yn+1），
∴点Pn的坐标为（xn，yn+1）
∴Q1(1，1)，P(1，
) ，Q2(
，
)．-----------------------------------（2分）
（2）∵Qn，Qn+1在曲线C上，
∴yn=
，yn+1=
，
又∵Pn在曲线Cn上，
∴yn+1=
，--------------------------------（4分）
∴xn+1=xn+2-n，
∴an=2-n．-----------------------------------------（6分）
（3）xn=（xn-xn-1）+（xn-1-xn-2）+…+（x2-x1）+x1
=2-（n-1）+2-（n-2）+…+2-1+1
=1-
=2-21-n．-------------------（9分）
∴an•bn=（xn+1-xn）•（yn-yn+1）
=2-n(
-
)
=
(
-
)
=
，
∵2•2n-2≥2n，2•2n-1≥3，
∴an•bn≤
．--------------------------------（12分）
∴Sn=a1b1+a2b2+…+anbn
≤
+
+…+
=
•
=
(1-
)＜
-----------------------（14分）
∴点Pn的坐标为（xn，yn+1）
∴Q1(1，1)，P(1，
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
（2）∵Qn，Qn+1在曲线C上，
∴yn=
| 1 |
| xn |
| 1 |
| xn+1 |
又∵Pn在曲线Cn上，
∴yn+1=
| 1 |
| xn+2-n |
∴xn+1=xn+2-n，
∴an=2-n．-----------------------------------------（6分）
（3）xn=（xn-xn-1）+（xn-1-xn-2）+…+（x2-x1）+x1
=2-（n-1）+2-（n-2）+…+2-1+1
=1-
1-(
| ||
1-
|
=2-21-n．-------------------（9分）
∴an•bn=（xn+1-xn）•（yn-yn+1）
=2-n(
| 1 |
| xn |
| 1 |
| xn+1 |
=
| 1 |
| 2n |
| 1 |
| 2-21-n |
| 1 |
| 2-2-n |
=
| 1 |
| (2•2n-2)• (2•2n-1) |
∵2•2n-2≥2n，2•2n-1≥3，
∴an•bn≤
| 1 |
| 3•2n |
∴Sn=a1b1+a2b2+…+anbn
≤
| 1 |
| 3×2 |
| 1 |
| 3×22 |
| 1 |
| 3×2n |
| 1 |
| 6 |
1-(
| ||
1-
|
| 1 |
| 3 |
| 1 |
| 2n |
| 1 |
| 3 |
点评：本题考查点坐标的求法、求数列的通项公式、求证sn＜
．解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化．
| 1 |
| 3 |
练习册系列答案
启东小题作业本系列答案
相关题目
如图，已知曲线
如图，已知曲线C：
（2006•南京二模）如图，已知曲线C：
如图，已知曲线C：y=x2（0≤x≤1），O（0，0），Q（1，0），R（1，1）．取线段OQ的中点A1，过A1作x轴的垂线交曲线C于P1，过P1作y轴的垂线交RQ于B1，记a1为矩形A1P1B1Q的面积．分别取线段OA1，P1B1的中点A2，A3，过A2，A3分别作x轴的垂线交曲线C于P2，P3，过P2，P3分别作y 轴的垂线交A1P1，RB1于B2，B3，记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和．以此类推，记an为2n-1个矩形面积之和，从而得数列{an}，设这个数列的前n项和为Sn．