Question

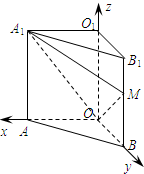（2009•闵行区一模）如图，直三棱柱OAB-O₁A₁B₁中，∠AOB=90°，M是侧棱BB₁上一点，向量

a

=(1，  1，  -1)是平面OA₁M的一个法向量，则平面OAB与平面OA₁M所成二面角的锐角为

arccos

3

3

（结果用反三角函数值表示）．

Answer 1

分析：由已知中，向量

a

=(1，  1，  -1)是平面OA₁M的一个法向量，结合直三棱柱OAB-O₁A₁B₁中，∠AOB=90°，易得

b

=（0，0，1）为面OAB的一个法向量，代入向量夹角公式，求出平面OAB与平面OA₁M所成二面角的锐角的余弦值，进而可用反三角函数表示出平面OAB与平面OA₁M所成二面角的锐角．

解答：解：∵棱柱OAB-O₁A₁B₁为直三棱柱
∴OO₁⊥平面∠OAB，
结合∠AOB=90°，可以以O的坐标原点，建立如图空间坐标系
则

b

=（0，0，1）为面OAB的一个法向量
又∵向量

a

=(1，  1，  -1)是平面OA₁M的一个法向量
设平面OAB与平面OA₁M所成二面角的锐角为θ，则
cosθ=

| a • b |

| a |•| b |

=

3

3

故平面OAB与平面OA₁M所成二面角的锐角为arccos

3

3

故答案为：arccos

3

3

点评：本题考查的知识点是与二面角有关的立体几何综合题，其中建立空间坐标系，将二面角问题转化为向量夹角问题是解答本题的关键，在解答中易忽略所求出平面OAB与平面OA₁M所成二面角的锐角，而错解为arccos-

3

3

．