题目内容
(2009•闵行区一模)在平面直角坐标系xOy中,以Ox轴为始边作锐角α,其终边与单位圆相交于A点,若A点的横坐标
,则tan(
+
)的值为
| 4 |
| 5 |
| α |
| 2 |
| π |
| 4 |
2
2
.分析:根据题意画出图形,作AB垂直于x轴,由单位圆的半径为1,且A的横坐标,根据勾股定理求出|AB|的长,即为A的纵坐标,根据锐角三角函数定义可知tanα的值为AB:OB,求出tanα的值,然后利用二倍角的正切函数公式化简tanα,根据其值得到关于tan
的方程,求出方程的解得到tan
的值,最后把所求式子利用两角和与差的正切函数公式及特殊角的三角函数值化简后,将tan
的值代入即可求出值.
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
解答:解:根据题意画出图形,如图所示:
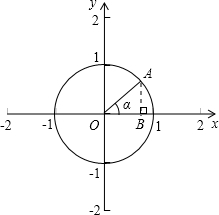
过A作AB⊥x轴,
∵A点的横坐标
,即|OB|=
,又|OA|=1,
在Rt△AOB中,根据勾股定理得:|AB|=
,
∴A的纵坐标为
,即tanα=
,
∴tanα=
=
,即(3tan
-1)(tan
+3)=0,
解得:tanα=
或tanα=-3(舍去),
则tan(
+
)=
=2.
故答案为:2

过A作AB⊥x轴,
∵A点的横坐标
| 4 |
| 5 |
| 4 |
| 5 |
在Rt△AOB中,根据勾股定理得:|AB|=
| 3 |
| 5 |
∴A的纵坐标为
| 3 |
| 5 |
| 3 |
| 4 |
∴tanα=
2tan
| ||
1-tan2
|
| 3 |
| 4 |
| α |
| 2 |
| α |
| 2 |
解得:tanα=
| 1 |
| 3 |
则tan(
| α |
| 2 |
| π |
| 4 |
| ||
1-
|
故答案为:2
点评:此题考查了锐角三角函数定义,二倍角的正切函数公式,两角和与差的正切函数公式,以及特殊角的三角函数值,利用了数形结合的思想,熟练运用公式是解本题的关键.

练习册系列答案
相关题目