题目内容
【题目】已知抛物线![]() 上两点
上两点![]() 、
、![]() ,焦点
,焦点![]() 满足
满足![]() ,线段
,线段![]() 的垂直平分线过
的垂直平分线过![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() ,使得抛物线
,使得抛物线![]() 上恰有三个点到直线
上恰有三个点到直线![]() 的距离都为
的距离都为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() ,结合抛物线的定义得出
,结合抛物线的定义得出![]() ,再由中垂线的性质得出
,再由中垂线的性质得出![]() ,利用两点间的距离公式得出
,利用两点间的距离公式得出![]() ,可求出实数
,可求出实数![]() 的值,由此可得出抛物线
的值,由此可得出抛物线![]() 的方程;
的方程;
(2)设直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 平移且使得平移后的直线与直线
平移且使得平移后的直线与直线![]() 之间的距离等于
之间的距离等于![]() ,可得出直线
,可得出直线![]() ,
,![]() ,可知直线
,可知直线![]() 或
或![]() 与抛物线
与抛物线![]() 相切,并与抛物线
相切,并与抛物线![]() 的方程联立,利用
的方程联立,利用![]() 求出实数
求出实数![]() 的值,即可得出直线
的值,即可得出直线![]() 的方程.
的方程.
(1)由抛物线的定义可得![]() ,①
,①
由于线段![]() 的垂直平分线过
的垂直平分线过![]() ,则
,则![]() ,
,
即![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,②
,②
由①②得![]() ,因此,抛物线
,因此,抛物线![]() 的方程为
的方程为![]() ;
;
(2)设直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 平移且使得平移后的直线与直线
平移且使得平移后的直线与直线![]() 之间的距离等于
之间的距离等于![]() ,设平移后的直线方程为
,设平移后的直线方程为![]() ,由平行线间的距离公式可得
,由平行线间的距离公式可得![]() ,
,
得![]() ,得直线
,得直线![]() ,
,![]() ,
,
可知直线![]() 或
或![]() 与抛物线
与抛物线![]() 相切,
相切,
若直线![]() 与抛物线
与抛物线![]() 相切,则
相切,则 ,得
,得![]() ,
,
![]() ,此方程无解;
,此方程无解;
若直线![]() 与抛物线
与抛物线![]() 相切,则
相切,则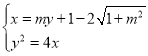 ,得
,得![]() ,
,
![]() ,得
,得![]() ,解得
,解得![]() ,
,
因此,直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 | 不满意 | |
男顾客 | 40 | 10 |
女顾客 | 30 | 20 |
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附:![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |





