题目内容
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.A.选修4-1:几何证明选讲
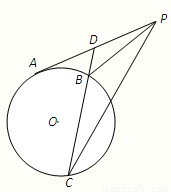
如图,PA切⊙O于点A,D为PA的中点,过点D引割线交⊙O于B、C两点.求证:∠DPB=∠DCP.
B.选修4-2:矩阵与变换
设M=
 ,N=
,N=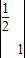 ,试求曲线y=sinx在矩阵MN变换下的曲线方程.
,试求曲线y=sinx在矩阵MN变换下的曲线方程.C.选修4-4:坐标系与参数方程
在极坐标系中,圆C的极坐标方程为
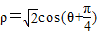 ,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为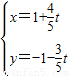 (t为参数),求直线l被圆C所截得的弦长.
(t为参数),求直线l被圆C所截得的弦长.D.选修4-5:不等式选讲
解不等式:|2x+1|-|x-4|<2.
【答案】分析:A先根据条件得到DP2=DB•DC;进而得到△BDP∽△PDC即可得到结论;
B 先求出MN,再设(x,y)是曲线y=sinx上的任意一点,在矩阵MN变换下对应的点为(a,b).根据矩阵变换得到即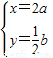 ,再代入原函数即可得到结论.
,再代入原函数即可得到结论.
C 把曲线的极坐标方程化为直角坐标方程可得分别表示圆和一条直线,利用点到直线的距离公式可得弦心距,最后结合弦长公式即可得到结论.
D 分情况去绝对值,分别求解即可.
解答:选做题
A.证明:因为PA与圆相切于A,
所以DA2=DB•DC,…(2分)
因为D为PA中点,所以DP=DA,
所以DP2=DB•DC,即 . …(5分)
. …(5分)
因为∠BDP=∠PDC,所以△BDP∽△PDC,…(8分)
所以∠DPB=∠DCP. …(10分)
B.MN=
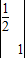 =
=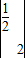 ,…(4分)
,…(4分)
设(x,y)是曲线y=sinx上的任意一点,在矩阵MN变换下对应的点为(a,b).
则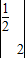
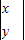 =
= ,所以
,所以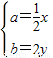 即
即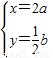 …(8分)
…(8分)
代入y=sinx得: b=sin2a,即b=2sin2a.
b=sin2a,即b=2sin2a.
即曲线y=sinx在矩阵MN变换下的曲线方程为y=2sin2x. …(10分)
C.曲线C的极坐标方程ρ=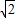 cos(θ+
cos(θ+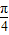 )=cosθ-sinθ,
)=cosθ-sinθ,
化为直角坐标方程为x2+y2-x+y=0,即(x- )2+(y+
)2+(y+ )2=
)2= .…(3分)
.…(3分)
直线L: ,(t为参数)可化为3x+4y+1=0,…(6分)
,(t为参数)可化为3x+4y+1=0,…(6分)
圆心到直线的距离d=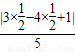 =
=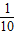 ,…(8分)
,…(8分)
弦长L=2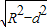 =
= ..…(10分)
..…(10分)
D.当x≥4时,2x+1-x+4<2,解得x<-3(舍去);…(3分)
当- ≤x<4时,2x+1+x-4<2,解得x<
≤x<4时,2x+1+x-4<2,解得x< ,∴-
,∴- ≤x<
≤x< ;…(6分)
;…(6分)
当x<- 时,-2x-1+x-4<2,解得x>-7,∴-7<x<-
时,-2x-1+x-4<2,解得x>-7,∴-7<x<- .…(9分)
.…(9分)
综上,不等式的解集为(-7, ).…(10分)
).…(10分)
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,简单的矩阵运算和绝对值不等式的解法,属于基础题.
B 先求出MN,再设(x,y)是曲线y=sinx上的任意一点,在矩阵MN变换下对应的点为(a,b).根据矩阵变换得到即
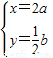 ,再代入原函数即可得到结论.
,再代入原函数即可得到结论.C 把曲线的极坐标方程化为直角坐标方程可得分别表示圆和一条直线,利用点到直线的距离公式可得弦心距,最后结合弦长公式即可得到结论.
D 分情况去绝对值,分别求解即可.
解答:选做题
A.证明:因为PA与圆相切于A,
所以DA2=DB•DC,…(2分)
因为D为PA中点,所以DP=DA,
所以DP2=DB•DC,即
 . …(5分)
. …(5分)因为∠BDP=∠PDC,所以△BDP∽△PDC,…(8分)
所以∠DPB=∠DCP. …(10分)
B.MN=

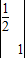 =
=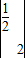 ,…(4分)
,…(4分)设(x,y)是曲线y=sinx上的任意一点,在矩阵MN变换下对应的点为(a,b).
则
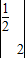
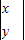 =
= ,所以
,所以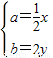 即
即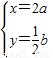 …(8分)
…(8分)代入y=sinx得:
 b=sin2a,即b=2sin2a.
b=sin2a,即b=2sin2a.即曲线y=sinx在矩阵MN变换下的曲线方程为y=2sin2x. …(10分)
C.曲线C的极坐标方程ρ=
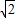 cos(θ+
cos(θ+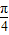 )=cosθ-sinθ,
)=cosθ-sinθ,化为直角坐标方程为x2+y2-x+y=0,即(x-
 )2+(y+
)2+(y+ )2=
)2= .…(3分)
.…(3分)直线L:
 ,(t为参数)可化为3x+4y+1=0,…(6分)
,(t为参数)可化为3x+4y+1=0,…(6分)圆心到直线的距离d=
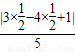 =
=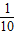 ,…(8分)
,…(8分)弦长L=2
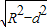 =
= ..…(10分)
..…(10分)D.当x≥4时,2x+1-x+4<2,解得x<-3(舍去);…(3分)
当-
 ≤x<4时,2x+1+x-4<2,解得x<
≤x<4时,2x+1+x-4<2,解得x< ,∴-
,∴- ≤x<
≤x< ;…(6分)
;…(6分)当x<-
 时,-2x-1+x-4<2,解得x>-7,∴-7<x<-
时,-2x-1+x-4<2,解得x>-7,∴-7<x<- .…(9分)
.…(9分)综上,不等式的解集为(-7,
 ).…(10分)
).…(10分)点评:本题主要考查把极坐标方程化为直角坐标方程的方法,简单的矩阵运算和绝对值不等式的解法,属于基础题.

练习册系列答案
相关题目
 (选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤. 选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).
选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).