题目内容
18.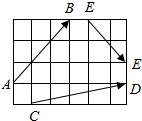 图中,小正方形的边长为1,则|$\overrightarrow{AB}$|=$3\sqrt{2}$,|$\overrightarrow{CD}$|=$\sqrt{26}$,|$\overrightarrow{EF}$|=$2\sqrt{2}$.
图中,小正方形的边长为1,则|$\overrightarrow{AB}$|=$3\sqrt{2}$,|$\overrightarrow{CD}$|=$\sqrt{26}$,|$\overrightarrow{EF}$|=$2\sqrt{2}$.
分析 直接利用向量与正方形的边长关系,求解模即可.
解答 解:由题意可知:|$\overrightarrow{AB}$|=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$.
|$\overrightarrow{CD}$|=$\sqrt{{5}^{2}+{1}^{2}}$=$\sqrt{26}$.
|$\overrightarrow{EF}$|=$\sqrt{{2}^{2}+(-2)^{2}}$=$2\sqrt{2}$.
故答案为:3$\sqrt{2}$;$\sqrt{26}$;2$\sqrt{2}$.
点评 本题考查向量的模的求法,考查计算能力.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
8.$\sqrt{14-6\sqrt{5}}$+$\root{3}{(\sqrt{5}-3)^{3}}$+$\root{4}{(-4)^{2}}$的值为( )
| A. | 8-2$\sqrt{5}$ | B. | 2$\sqrt{5}$-4 | C. | 2 | D. | 4 |
9.下列函数中,满足关系f(x+y)=f(x)+f(y)的是( )
| A. | f(x)=x2 | B. | f(x)=x+$\frac{1}{4}$ | C. | f(x)=2x | D. | f(x)=$\frac{1}{x}$ |
3.函数f(x)=lnx-x2的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
10.已知A={x|1<x<2015},B={x|x≤a},若A?B,则实数a的取值范围为( )
| A. | a≥2015 | B. | a>2015 | C. | a≥1 | D. | a>1 |