题目内容
7.函数y=x-x2的值域是(-∞,$\frac{1}{4}$];函数y=x-x2(-1≤x≤1)的值域是[-2,$\frac{1}{4}$];函数y=$\frac{1}{x-{x}^{2}}$的值域是(-∞,0)∪[4,+∞).分析 对该函数配方:$y=-(x-\frac{1}{2})^{2}+\frac{1}{4}$,这样便可看出该函数在R上的值域,而在-1≤x≤1上,通过配方后的解析式即可看出x=-1时,该函数取最小值,x=$\frac{1}{2}$,取最大值,从而可以写出该函数在[-1,1]上的值域.而对于第三个函数,x-x2在分母上,首先根据前面$x-{x}^{2}≤\frac{1}{4}$,从而得到x-x2的范围:$x-{x}^{2}<0,或0<x-{x}^{2}≤\frac{1}{4}$,然后求出$\frac{1}{x-{x}^{2}}$的范围即可.
解答 解:y=x-${x}^{2}=-(x-\frac{1}{2})^{2}+\frac{1}{4}≤\frac{1}{4}$;
∴该函数的值域为($-∞,\frac{1}{4}$];
可以看出,x=-1时,y=x-x2取最小值-2,并可以取到最大值$\frac{1}{4}$;
∴该函数在[-1,1]上的值域为:$[-2,\frac{1}{4}]$;
∵$x-{x}^{2}≤\frac{1}{4}$;
∴x-x2<0,或$0<x-{x}^{2}≤\frac{1}{4}$;
∴$\frac{1}{x-{x}^{2}}<0$,或$\frac{1}{x-{x}^{2}}≥4$;
∴该函数的值域为:(-∞,0)∪[4,+∞).
故答案为:$(-∞,\frac{1}{4}]$,$[-2,\frac{1}{4}]$,(-∞,0)∪[4,+∞).
点评 考查函数值域的概念及求法,配方求二次函数值域的方法,以及根据不等式的性质求函数值域的方法.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
2.下列函数中,值域是(0,+∞)的是( )
| A. | y=2-x(x<0) | B. | y=x2+2x+1 | C. | y=$\sqrt{{x}^{2}-4x+1}$ | D. | $\frac{1}{\sqrt{x}}$ |
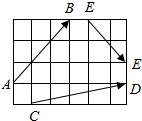 图中,小正方形的边长为1,则|$\overrightarrow{AB}$|=$3\sqrt{2}$,|$\overrightarrow{CD}$|=$\sqrt{26}$,|$\overrightarrow{EF}$|=$2\sqrt{2}$.
图中,小正方形的边长为1,则|$\overrightarrow{AB}$|=$3\sqrt{2}$,|$\overrightarrow{CD}$|=$\sqrt{26}$,|$\overrightarrow{EF}$|=$2\sqrt{2}$.