题目内容
已知实数x,y满足条件
,若使z=ax+y(a>0)取得最大值的最优解有无数个,则a值为
|
1
1
.分析:不等式组表示的平面区域如图,z=ax+y的几何意义是直线y=-ax+z的纵截距,利用z=ax+y取得最大值时的最优解(x,y)有无数个,可得y=-ax+z与直线y+x+1=0平行,故可求a的值.
解答:解:不等式组表示的平面区域如图,z=ax+y的几何意义是直线y=-ax+z的纵截距,
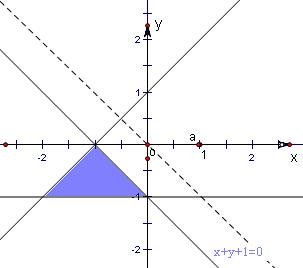
∵z=ax+y取得最大值时的最优解(x,y)有无数个,
∴y=-ax+z与直线y+x+1=0平行
∴a=1
故答案为:1.

∵z=ax+y取得最大值时的最优解(x,y)有无数个,
∴y=-ax+z与直线y+x+1=0平行
∴a=1
故答案为:1.
点评:本题考查线性规划知识,考查最优解,考查数形结合的数学思想.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 (x∈z,y∈z),每一对整数(x,y)对应平面上一个点,经过其中任意两点作直线,则不同直线的条数是( )
(x∈z,y∈z),每一对整数(x,y)对应平面上一个点,经过其中任意两点作直线,则不同直线的条数是( ) ,每一对整数(x,y)对应平面上一个点,则过这些点中的其中两个点可作 条不同的直线.
,每一对整数(x,y)对应平面上一个点,则过这些点中的其中两个点可作 条不同的直线. (x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,经过其中任意两点作直线,则不同直线的条数是
(x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,经过其中任意两点作直线,则不同直线的条数是