题目内容
已知实数x、y满足
(x∈z,y∈z),每一对整数(x,y)对应平面上一个点,经过其中任意两点作直线,则不同直线的条数是( )
|
| A、14 | B、19 | C、36 | D、72 |
分析:画出可行域,找出可行域中的整数点,利用组合求出构成的直线的条数,去掉重合的情况.
解答:解:作出不等式组
可行域
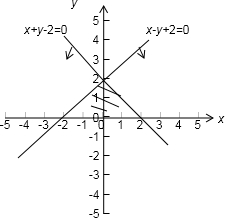
可行域中所有的整数点有(-2,0); (-1,0)(-1,1);(0,0);(0,1);(0,2);(1,0);(1,1);(2,0)
经过其中任意两点作直线,则不同直线的条数是C92-C52+1-C32+1-C32+1-
+1-
+1=19
故选B
|

可行域中所有的整数点有(-2,0); (-1,0)(-1,1);(0,0);(0,1);(0,2);(1,0);(1,1);(2,0)
经过其中任意两点作直线,则不同直线的条数是C92-C52+1-C32+1-C32+1-
| C | 2 3 |
| C | 2 3 |
故选B
点评:求完成某事件的方法数常用的方法是排列、组合的方法有时还用列举的方法.

练习册系列答案
相关题目
已知实数x,y满足
-
=1(a>0,b>0),则下列不等式中恒成立的是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、|y|<
| ||
B、y>-
| ||
C、|y|>-
| ||
D、y<
|