题目内容
已知函数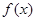 是
是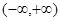 上的偶函数,若对于
上的偶函数,若对于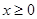 ,都有
,都有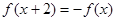 ,且当
,且当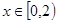 时,
时, 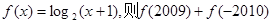 的值为 ()
的值为 ()
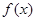 是
是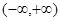 上的偶函数,若对于
上的偶函数,若对于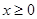 ,都有
,都有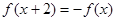 ,且当
,且当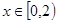 时,
时, 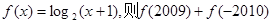 的值为 ()
的值为 ()| A.-2 | B.-1 | C.1 | D.2 |
C
分析:由偶函数的性质及函数的周期性将f(2009)+f(-2010)的值用x∈[0,2)时上的函数值表示出来,代入解析式求出值
解答:解:∵数f(x)是(-∞,+∞)上的偶函数,且对于x≥0,都有f(x+2)=f(x),
∴f(2009)+f(-2010)=f(2009)+f(2010)=f(1)+f(0)
又当x∈[0,2)时,f(x)=log2(x+1),
∴f(2009)+f(-2010)=f(1)+f(0)=log2(1)+log2(1+1)=1,
故选C.
点评:本题考查函数的周期性与函数偶函数的性质,解题的关键是根据函数的这两个性质灵活转化,将要求函数值用已知解析式的区间上的函数值表示出来,这是函数周期性运用的一种主要类型,题后应总结其规律,以便于做题时推广.
解答:解:∵数f(x)是(-∞,+∞)上的偶函数,且对于x≥0,都有f(x+2)=f(x),
∴f(2009)+f(-2010)=f(2009)+f(2010)=f(1)+f(0)
又当x∈[0,2)时,f(x)=log2(x+1),
∴f(2009)+f(-2010)=f(1)+f(0)=log2(1)+log2(1+1)=1,
故选C.
点评:本题考查函数的周期性与函数偶函数的性质,解题的关键是根据函数的这两个性质灵活转化,将要求函数值用已知解析式的区间上的函数值表示出来,这是函数周期性运用的一种主要类型,题后应总结其规律,以便于做题时推广.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
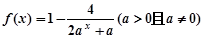 是定义在
是定义在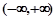 上的奇函数.
上的奇函数.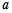 的值;(2)求函数
的值;(2)求函数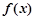 的值域;
的值域;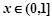 时,
时,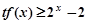 恒成立,求实数
恒成立,求实数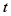 的取值范围.
的取值范围.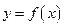 是定义在
是定义在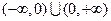 上的奇函数,当
上的奇函数,当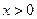 时,
时,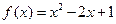 。
。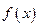 的解析式;
的解析式;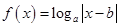 在
在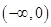 上是递增函数,则
上是递增函数,则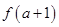 与
与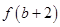 的大小关系是( )
的大小关系是( )
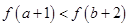

 数
数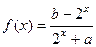 是奇函数
是奇函数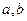 的值;
的值;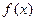 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;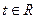 ,不等式
,不等式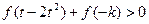 恒成立,求实数
恒成立,求实数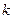 的取值范围。
的取值范围。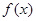 是
是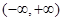 上的偶函数,若对于
上的偶函数,若对于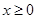 ,都有
,都有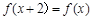 ,且当
,且当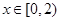 时,
时,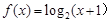 ,则
,则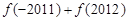 的值为
的值为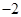
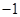
 在
在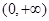 上是增函数,且
上是增函数,且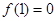 ,则不等式
,则不等式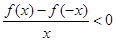
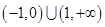
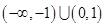
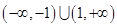
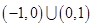
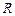 上的奇函数
上的奇函数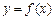 满足
满足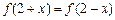 ,当
,当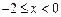 时,
时,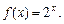 若
若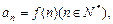 则
则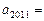 .
.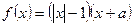 为奇函数,则
为奇函数,则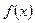 增区间为_______
增区间为_______