题目内容
6.若关于x的方程4-x2=|x-a|有负的实数根,则a的取值范围为( )| A. | [-$\frac{17}{4}$,$\frac{17}{4}$] | B. | (-$\frac{17}{4}$,$\frac{17}{4}$) | C. | [-$\frac{17}{4}$,4) | D. | [-$\frac{17}{4}$,4] |
分析 由题意可得直线y=x-a和y=4-x2=相切于y轴的左侧时,满足条件,易得a=-$\frac{17}{4}$,当直线经y=-x+a过点(0,4)时,此时,a=4,不满足条件,从而求得a的范围
解答 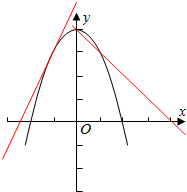 解:如图:由题意可得直线y=x-a和y=4-x2=相切于y轴的左侧时,满足条件,易得a=-$\frac{17}{4}$,
解:如图:由题意可得直线y=x-a和y=4-x2=相切于y轴的左侧时,满足条件,易得a=-$\frac{17}{4}$,
当直线经y=-x+a过点(0,4)时,此时,a=4,不满足条件,
故a的范围是[-$\frac{17}{4}$,4),
故选:C.
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
16.己知f(x)=x2-2x+2,在[$\frac{1}{4}$,m2-m+2]上任取三个数a,b,c,均存在以 f(a),f(b),f(c)为三边的三角形,则m的取值范围为( )
| A. | (0,1) | B. | [0,$\frac{\sqrt{2}}{2}$) | C. | (0,$\frac{\sqrt{2}}{2}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] |
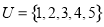 , 集合
, 集合 ,
, 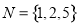 , 则集合
, 则集合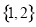 可以表示为
可以表示为 B.
B.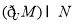
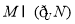 D.
D.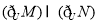
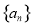 满足
满足 ( )
( ) B.
B.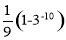 C.
C. D.
D.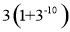
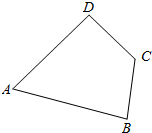 如图,A,B,C,D为平面四边形ABCD的四个内角.
如图,A,B,C,D为平面四边形ABCD的四个内角.