题目内容
已知向量a=(2,1),b=(x,y).
(1)若x∈{-1,0,1,2},y∈{-1,0,1},求向量a∥b的概率;
(2)若x∈[-1,2],y∈[-1,1],求向量a,b的夹角是钝角的概率.
(1)若x∈{-1,0,1,2},y∈{-1,0,1},求向量a∥b的概率;
(2)若x∈[-1,2],y∈[-1,1],求向量a,b的夹角是钝角的概率.
(1)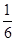 (2)
(2)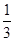
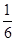 (2)
(2)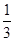
(1)设“a∥b”为事件A,由a∥b,得x=2y.
基本事件空间为Ω={(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),(2,-1),(2,0),(2,1)},共包含12个基本事件;
其中A={(0,0),(2,1)},包含2个基本事件.
则P(A)=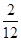 =
=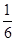 ,即向量a∥b的概率为
,即向量a∥b的概率为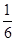 .
.
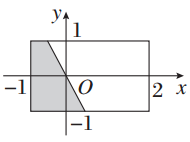
(2)设“a,b的夹角是钝角”为事件B,由a,b的夹角是钝角,可得a·b<0,即2x+y<0,且x≠2y.基本事件空间为Ω={(x,y)|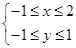 },
},
B={(x,y)|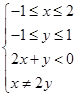 },
},
则由图可知,P(B)=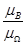 =
=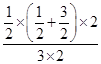 =
=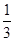 ,
,
即向量a,b的夹角是钝角的概率是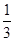 .
.
基本事件空间为Ω={(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),(2,-1),(2,0),(2,1)},共包含12个基本事件;
其中A={(0,0),(2,1)},包含2个基本事件.

则P(A)=
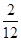 =
=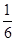 ,即向量a∥b的概率为
,即向量a∥b的概率为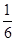 .
.(2)设“a,b的夹角是钝角”为事件B,由a,b的夹角是钝角,可得a·b<0,即2x+y<0,且x≠2y.基本事件空间为Ω={(x,y)|
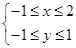 },
},B={(x,y)|
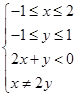 },
},则由图可知,P(B)=
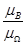 =
=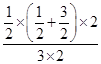 =
=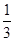 ,
,即向量a,b的夹角是钝角的概率是
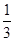 .
.
练习册系列答案
相关题目

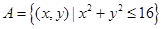 和集
和集 表示的平面区域分别为
表示的平面区域分别为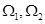 .若在区域
.若在区域 内任取一点
内任取一点 ,则点
,则点 落在区域
落在区域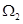 的概率为( )
的概率为( )

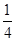
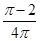
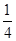

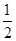
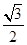
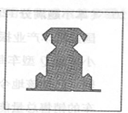
 则点
则点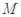 取自阴影部分的概率为 。
取自阴影部分的概率为 。
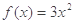 )
)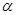 ,则
,则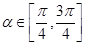 的概率为 .
的概率为 .