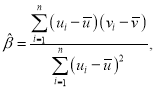题目内容
【题目】如图,三棱柱![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点.
的中点.
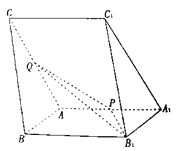
(1)在![]() 上确定点M,使
上确定点M,使![]() 平面
平面![]() ,并说明理由。
,并说明理由。
(2)若侧面![]() 侧面
侧面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
【答案】(1)答案见解析;(2)![]() .
.
【解析】
(1)取BC中点M,连接AM,则AM∥平面PQB1;利用面面平行证明线面平行即可;
(2)作QO⊥平面ABB1A1,与A1A延长线交于O,作PN∥C1A1,则直线A1C1与平面PQB1所成角即直线PN与平面PQB1所成角,结合几何关系求解直线![]() 与平面
与平面![]() 所成角的正弦值即可.
所成角的正弦值即可.
(1)取BC中点M,连接AM,则AM∥平面PQB1;
如图所示,取BB1中点N,连结AM,AN,
![]() 为平行四边形,点N,P为中点,则
为平行四边形,点N,P为中点,则![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面PQB1,
平面PQB1,
同理可得,![]() 平面PQB1,
平面PQB1,
据此可得平面AMN∥平面PQB1,故![]() 平面
平面![]() .
.

(2)作QO⊥平面ABB1A1,与A1A延长线交于O,

则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
作PN∥C1A1,则直线A1C1与平面PQB1所成角即直线PN与平面PQB1所成角,
![]() .
.
设N到平面PQB1的距离为h,则![]() ,
,
∴直线A1C1与平面PQB1所成角的正弦值为:![]() .
.

【题目】某市房产中心数据研究显示,2018年该市新建住宅销售均价如下表.3月至7月房价上涨过快,为抑制房价过快上涨,政府从8月份开始出台了相关限购政策,10月份开始房价得到了很好的抑制.
均价(万元/ | 0.95 | 0.98 | 1.11 | 1.12 | 1.20 | 1.22 | 1.32 | 1.34 | 1.16 | 1.06 |
月份 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
(Ⅰ)请建立3月至7月线性回归模型(保留小数点后3位),并预测若政府不宏观调控,12月份该市新建住宅销售均价;
(Ⅱ)试用相关系数说明3月至7月各月均价![]() (万元/
(万元/![]() )与月份
)与月份![]() 之间可用线性回归模型(保留小数点后2位)
之间可用线性回归模型(保留小数点后2位)
参考数据:![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
回归方程斜率和截距最小二乘法估计公式 ;
;
相关系数 .
.