题目内容
已知函数f(x)= mcos2
mcos2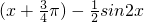 .
.
(1)若m=1,求函数f(x)的最值;
(2)若函数f(x)在区间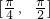 上的最小值等于2,求实数m的值.
上的最小值等于2,求实数m的值.
解:(1)当m=1时,f(x)= cos2
cos2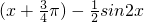
=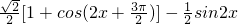
=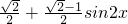
∵-1≤sin2x≤1
∴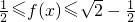
∴函数的最大值为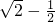 ,最小值为
,最小值为
(2)∵f(x)= cos2
cos2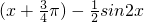 =
=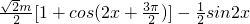
=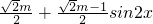
∵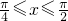
∴ ,0≤sin2x≤1
,0≤sin2x≤1
当m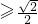 时,由题意可得
时,由题意可得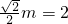 ,则m=
,则m=
当m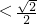 时,由题意可得
时,由题意可得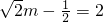 ,此时m不存在
,此时m不存在
综上可得m=2
分析:(1)当m=1时,f(x)= cos2
cos2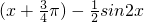 =
=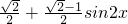 ,结合-1≤sin2x≤1可求
,结合-1≤sin2x≤1可求
(2)利用二倍角公式、辅助角公式、诱导公式对函数化简f(x)= cos2
cos2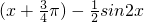 =
=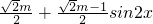 结合x的范围可求,sin2x的范围,结合
结合x的范围可求,sin2x的范围,结合 的正负可求函数取得最小值时的m
的正负可求函数取得最小值时的m
点评:本题主要考察了二倍角公式、辅助角公式及诱导公式在三角函数化简中的应用,正弦函数的性质的灵活应用是解答本题的关键
 cos2
cos2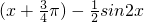
=
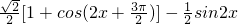
=
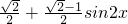
∵-1≤sin2x≤1
∴
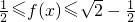
∴函数的最大值为
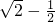 ,最小值为
,最小值为
(2)∵f(x)=
 cos2
cos2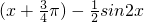 =
=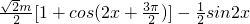
=
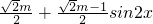
∵
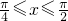
∴
 ,0≤sin2x≤1
,0≤sin2x≤1当m
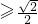 时,由题意可得
时,由题意可得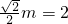 ,则m=
,则m=
当m
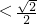 时,由题意可得
时,由题意可得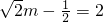 ,此时m不存在
,此时m不存在综上可得m=2

分析:(1)当m=1时,f(x)=
 cos2
cos2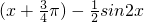 =
=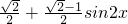 ,结合-1≤sin2x≤1可求
,结合-1≤sin2x≤1可求(2)利用二倍角公式、辅助角公式、诱导公式对函数化简f(x)=
 cos2
cos2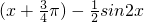 =
=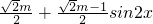 结合x的范围可求,sin2x的范围,结合
结合x的范围可求,sin2x的范围,结合 的正负可求函数取得最小值时的m
的正负可求函数取得最小值时的m点评:本题主要考察了二倍角公式、辅助角公式及诱导公式在三角函数化简中的应用,正弦函数的性质的灵活应用是解答本题的关键

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目