题目内容
函数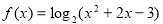
的单调减区间为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
A
【解析】
试题分析：要是函数
有意义的需要满足：
，解得
或
，所以函数的定义域为
；
令
，则
，因为函数在
是单调递增函数，由复合函数同增异减，要求函数的单调递减区间，即为函数的单调递减区间与函数定义域的交集；函数是开口向上，对称轴为
的二次函数，则函数的单调递减区间为
，所以函数的单调递减区间为
，所以答案选
.
考点：1.复合函数的单调性；2.对数函数的单调性；3.二次函数的单调性；4.函数的定义域；5.一元二次不等的解法.
练习册系列答案
备战中考寒假系列答案
相关题目
