题目内容
定义在 上的函数
上的函数 ,对任意
,对任意 都有
都有 ,当
,当 时,
时, ,则
,则 ________.
________.
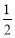
【解析】
试题分析:由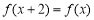 可知函数
可知函数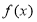 是周期函数且周期为
是周期函数且周期为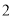 ;所以
;所以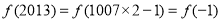 ,而当
,而当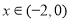 时,
时,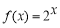 ,故
,故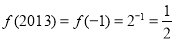 .
.
考点:1.函数的周期性;2.抽象函数;3.函数的解析式.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
题目内容
定义在 上的函数
上的函数 ,对任意
,对任意 都有
都有 ,当
,当 时,
时, ,则
,则 ________.
________.
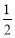
【解析】
试题分析:由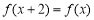 可知函数
可知函数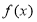 是周期函数且周期为
是周期函数且周期为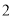 ;所以
;所以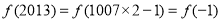 ,而当
,而当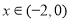 时,
时,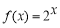 ,故
,故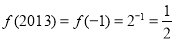 .
.
考点:1.函数的周期性;2.抽象函数;3.函数的解析式.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案