题目内容
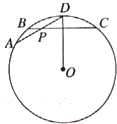（几何证明选讲选做题） 如图，半径为5的圆O的两条弦AD和BC相交于点P，OD⊥BC，P为AD的中点，BC=6，则弦AD的长度为________．
2
分析：由已知中半径为5的圆O的两条弦AD和BC相交于点P，OD⊥BC，P为AD的中点，BC=6，根据垂径定理，我们易求出OE及DE的长，连接OP后，又可以有垂径定理得到OP⊥AD，由射影定理求出OP后，即可求出弦AD的长度．
解答：连接OP，如下图所示：
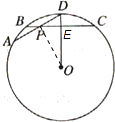
∵OD⊥BC，BC=6，圆的半径R=OD=OC=5
则BE=CE=3，OE=
=4，DE=1
又∵P为AD的中点，
∴OP⊥AD
在Rt△OPD中，由射影定理得
OP=
=2
∴DP=
∴AD=2
故答案为：2．
点评：本题考查的知识点是垂径定理，射影定理，圆的弦长公式，其中半弦长与半径及弦心距构造直角三角形，满足勾股定理是解答本题的关键．
分析：由已知中半径为5的圆O的两条弦AD和BC相交于点P，OD⊥BC，P为AD的中点，BC=6，根据垂径定理，我们易求出OE及DE的长，连接OP后，又可以有垂径定理得到OP⊥AD，由射影定理求出OP后，即可求出弦AD的长度．
解答：连接OP，如下图所示：
∵OD⊥BC，BC=6，圆的半径R=OD=OC=5
则BE=CE=3，OE=
=4，DE=1又∵P为AD的中点，
∴OP⊥AD
在Rt△OPD中，由射影定理得
OP=
=2∴DP=
∴AD=2
故答案为：2
．点评：本题考查的知识点是垂径定理，射影定理，圆的弦长公式，其中半弦长与半径及弦心距构造直角三角形，满足勾股定理是解答本题的关键．
练习册系列答案
相关题目
（几何证明选讲选做题）
（几何证明选讲选做题）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，直线MN切⊙O于D，∠MDA=60°，则∠BCD=
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（几何证明选讲选做题）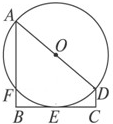
（几何证明选讲选做题）