题目内容
14.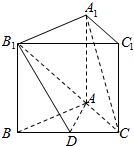 已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.
已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.(1)当D在何处时,A1C∥平面AB1D,并证明之.
(2)若D为BC中点,且直线AB1与平面ABC成60°角,试求二面角B-AB1-D的余弦值大小.
分析 (1)连结A1B,交AB1于点O,由三角形中位线定理得OD∥A1C,由此得到D在BC中点时,A1C∥平面AB1D.
(2)由已知得到∠BAB1=60°,BB1=$\sqrt{3}$,取B1C1中点E,以D为原点,AD为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,利用向量法能求出二面角B-AB1-D的余弦值.
解答 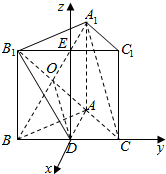 解:(1)当D为BC中点时,A1C∥平面AB1D.
解:(1)当D为BC中点时,A1C∥平面AB1D.
证明如下:
连结A1B,交AB1于点O,则O为A1B的中点,
连结OD,∵D是BC中点,∴OD∥A1C,
∵A1C?平面AB1D,OD?平面AB1D,
∴A1C∥平面AB1D.
(2)∵正三棱柱ABC-A1B1C1中,BC=1,
D为BC中点,且直线AB1与平面ABC成60°角,
∴∠BAB1=60°,∴AB1=2,BB1=$\sqrt{3}$,
取B1C1中点E,以D为原点,AD为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,
则A(-$\sqrt{3}$,0,0),B(0,-$\frac{1}{2}$,0),D(0,0,0),B1(0,-$\frac{1}{2}$,$\sqrt{3}$),
$\overrightarrow{AB}$=($\sqrt{3}$,-$\frac{1}{2}$,0),$\overrightarrow{A{B}_{1}}$=($\sqrt{3},-\frac{1}{2},\sqrt{3}$),$\overrightarrow{DA}=(-\sqrt{3},0,0)$,$\overrightarrow{D{B}_{1}}$=(0,-$\frac{1}{2}$,$\sqrt{3}$),
设平面ABB1的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=\sqrt{3}x-\frac{1}{2}y=0}\\{\overrightarrow{n}•\overrightarrow{A{B}_{1}}=\sqrt{3}x-\frac{1}{2}y+\sqrt{3}z=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{n}$=($\sqrt{3}$,6,0),
充平面AB1D的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DA}=-\sqrt{3}a=0}\\{\overrightarrow{m}•\overrightarrow{D{B}_{1}}=-\frac{1}{2}b+\sqrt{3}c=0}\end{array}\right.$,取c=$\sqrt{3}$,得$\overrightarrow{m}$=(0,6,$\sqrt{3}$),
设二面角B-AB1-D的平面角为θ,
cosθ=|cos<$\overrightarrow{m},\overrightarrow{n}$>|=|$\frac{36}{\sqrt{39}•\sqrt{39}}$|=$\frac{12}{13}$,
∴二面角B-AB1-D的余弦值大小为$\frac{12}{13}$.
点评 本题考查使线面平行的点的位置的确定,考查二面角的余弦值的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | (1,2) | B. | (1,3] | C. | (2,3] | D. | (1,3) |
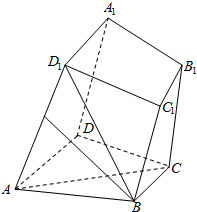 如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1
如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1