题目内容
【题目】已知函数f(x)=x+ ![]() ﹣4,g(x)=kx+3.
﹣4,g(x)=kx+3.
(1)当a=k=1时,求函数y=f(x)+g(x)的单调递增与单调递减区间;
(2)当a∈[3,4]时,函数f(x)在区间[1,m]上的最大值为f(m),试求实数m的取值范围;
(3)当a∈[1,2]时,若不等式|f(x1)|﹣|f(x2)|<g(x1)﹣g(x2)对任意x1 , x2∈[2,4](x1<x2)恒成立,求实数k的取值范围.
【答案】
(1)解:a=k=1时,y=f(x)+g(x)=2x+ ![]() ﹣1,
﹣1,
y′=2﹣ ![]() =
= ![]() ,
,
令y′>0,解得:x>1或x<﹣1,令y′<0,解得:﹣1<x<1且x≠0,
故函数在(﹣∞,﹣1)递增,在(﹣1,0),(0,1)递减,在(1,+∞)递增
(2)解:∵a∈[3,4],
∴y=f(x)在(1, ![]() )上递减,在(
)上递减,在( ![]() ,+∞)上递增,
,+∞)上递增,
又∵f(x)在区间[1,m]上的最大值为f(m),
∴f(m)≥f(1),解得(m﹣1)(m﹣a)≥0,
∴m≥amax,即m≥4
(3)解:∵|f(x1)|﹣|f(x2)|<g(x1)﹣g(x2),
∴|f(x1)|﹣g(x1)<|f(x2)|﹣g(x2)恒成立,
令F(x)=|f(x)|﹣g(x),则F(x)在[2,4]上递增.
对于F(x)= 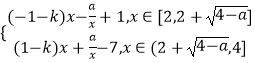 ,
,
(i)当x∈[2,2+ ![]() ]时,F(x)=(﹣1﹣k)x﹣
]时,F(x)=(﹣1﹣k)x﹣ ![]() +1,
+1,
①当k=﹣1时,F(x)=﹣ ![]() +1在[2,2+
+1在[2,2+ ![]() ]上递增,所以k=﹣1符合;
]上递增,所以k=﹣1符合;
②当k<﹣1时,F(x)=(﹣1﹣k)x﹣ ![]() +1在[2,2+
+1在[2,2+ ![]() ]上递增,所以k<﹣1符合;
]上递增,所以k<﹣1符合;
③当k>﹣1时,只需 ![]() ≥2+
≥2+ ![]() ,即
,即 ![]() ≥(
≥( ![]() +
+ ![]() )max=2+
)max=2+ ![]() ,
,
所以﹣1<k≤6﹣4 ![]() ,从而k≤6﹣4
,从而k≤6﹣4 ![]() ;
;
(ii)当x∈(2+ ![]() ,4]时,F(x)=(1﹣k)x+
,4]时,F(x)=(1﹣k)x+ ![]() ﹣7,
﹣7,
①当k=1时,F(x)= ![]() ﹣7在(2+
﹣7在(2+ ![]() ,4]上递减,所以k=1不符合;
,4]上递减,所以k=1不符合;
②当k>1时,F(x)=(1﹣k)x+ ![]() ﹣7在(2+
﹣7在(2+ ![]() ,4]上递减,所以k>1不符合;
,4]上递减,所以k>1不符合;
③当k<1时,只需 ![]() ≤2+
≤2+ ![]() ,即
,即 ![]() ≤(
≤( ![]() +
+ ![]() )min=1+
)min=1+ ![]() ,
,
所以k<2 ![]() ﹣2,
﹣2,
综上可知:k≤6﹣4 ![]()
【解析】(1)将a=k=1代入函数,求出函数y=f(x)+g(x)的导数,从而求出函数的单调区间即可;(2)解不等式f(m)≥f(1)即可;(3)不等式等价于F(x)=|f(x)|﹣g(x)在[2,4]上递增,显然F(x)为分段函数,结合单调性对每一段函数分析讨论即可.
【考点精析】利用利用导数研究函数的单调性和函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(1)求y关于t的回归方程 ![]() .
.
(2)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.
附:回归方程 ![]() 中
中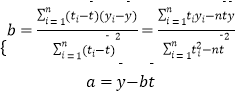 .
.