题目内容
已知直线l:y=kx+2(k为常数)过椭圆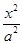 +
+ =1(a>b>0)的上顶点B和左焦点F,直线l被圆x2+y2=4截得的弦长为d.
=1(a>b>0)的上顶点B和左焦点F,直线l被圆x2+y2=4截得的弦长为d.
(1)若d=2 ,求k的值;
,求k的值;
(2)若d≥ ,求椭圆离心率e的取值范围.
,求椭圆离心率e的取值范围.
(1)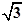 (2)0<e≤
(2)0<e≤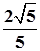 .
.
解析试题分析:解:(1)取弦的中点为M,连结OM由平面几何知识,OM=1,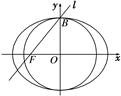
OM=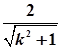 =1.解得k2=3,k=±
=1.解得k2=3,k=±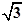 .
.
∵直线过F、B,∴k>0,则k=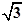 .
.
(2)设弦的中点为M,连结OM,则OM2=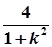 ,
,
d2=4(4-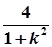 )≥(
)≥(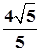 )2,解得k2≥
)2,解得k2≥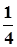 .
.
e2=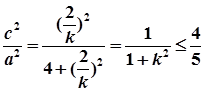 ,∴0<e≤
,∴0<e≤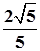 .
.
考点:椭圆的性质
点评:解决的关键是利用距离公式以及平面几何知识来得到不等式,点在椭圆内,求解k的范围,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
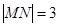 。椭圆D:
。椭圆D: 的焦距等于
的焦距等于 ,且过点
,且过点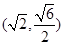

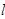 与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线
与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线 斜率的范围。
斜率的范围。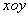 中,曲线
中,曲线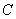 的参数方程为
的参数方程为 (
(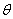 为参数)。
为参数)。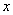 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为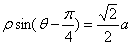 (其中
(其中 为常数)
为常数)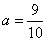 时,曲线
时,曲线 .求
.求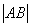 的值;
的值; 轴上的椭圆的离心率为
轴上的椭圆的离心率为 ,且经过点
,且经过点 。若分别过椭圆的左右焦点
。若分别过椭圆的左右焦点 、
、 的动直线
的动直线 、
、 相交于P点,与椭圆分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率
相交于P点,与椭圆分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率 、
、 、
、 、
、 满足
满足 .
.
 为定值.若存在,求出M、N点坐标;若不存在,说明理由.
为定值.若存在,求出M、N点坐标;若不存在,说明理由.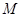 :
: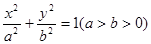 的离心率为
的离心率为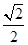 ,点
,点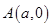 、
、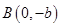 ,原点
,原点 到直线
到直线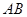 的距离为
的距离为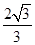 .
.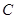
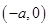 ,点
,点 在椭圆
在椭圆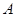 、
、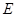 在直线
在直线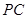 上,若直线
上,若直线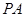 的方程为
的方程为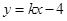 ,且
,且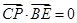 ,试求直线
,试求直线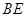 的方程.
的方程.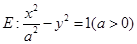 的离心率等于
的离心率等于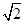 ,直线
,直线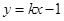 与双曲线
与双曲线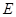 的右支交于
的右支交于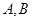 两点.
两点.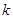 的取值范围;
的取值范围;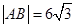 ,点
,点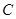 是双曲线
是双曲线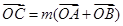 ,求
,求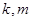
 的焦点
的焦点 作倾斜角为
作倾斜角为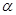 的直线交抛物线于
的直线交抛物线于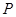 、
、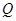 两点,过点
两点,过点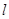 交
交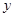 轴于点
轴于点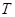 ,过点
,过点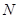 。
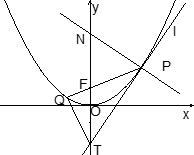
。
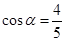 ,求此抛物线与线段
,求此抛物线与线段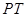 以及线段
以及线段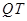 所围成的封闭图形的面积。
所围成的封闭图形的面积。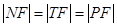 ;
;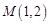 ,它们在
,它们在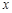 轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点.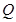 ,点
,点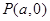 都满足
都满足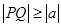 ,求
,求 的取值范围.
的取值范围. 与椭圆
与椭圆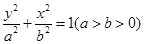 交于
交于 ,
, 两点,已知
两点,已知
 ,
,
 ,若
,若 且椭圆的离心率
且椭圆的离心率 ,又椭圆经过点
,又椭圆经过点 ,
, 为坐标原点.
为坐标原点. (
( 为半焦距),求直线
为半焦距),求直线 的值;
的值;