题目内容
13.若点A(-2,m)在正比例函数y=-$\frac{1}{2}$x的图象上,则m的值是( )| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 1 | D. | -1 |
分析 由已知条件把点A(-2,m)代入正比例函数y=-$\frac{1}{2}$x,能求出m.
解答 解:∵点A(-2,m)在正比例函数y=-$\frac{1}{2}$x的图象上,
∴m=-$\frac{1}{2}×(-2)$=1.
∴m的值是1.
故选:C.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意正比例函数的性质的合理运用.

练习册系列答案
相关题目
3.满足BC=1.5,AC=1,B=30°的不同△ABC有多少个( )
| A. | 两个 | B. | 一个 | C. | 零个 | D. | 无数个 |
1.若函数y=log${\;}_{\frac{1}{2}}$(3x2-6x十5)在[a,+∞)上是减函数,则实数a的取值范围是( )
| A. | [1,+∞) | B. | [2,+∞) | C. | (-∞,2] | D. | (-∞,1] |
1.将函数y=sin(2x-θ)的图象F向右平移$\frac{π}{3}$个单位长度得到图象F′,若F′的一条对称轴是直线x=$\frac{π}{4}$,则θ的一个可能取值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
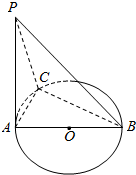 AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.
AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.