题目内容
4.已知点x,y满足不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{2x+y≤2}\end{array}\right.$,若ax+y≤3恒成立,则实数a的取值范围是(-∞,3].分析 画出不等式满足的平面区域,由ax+y≤3恒成立,结合图形确定出a的范围即可.
解答 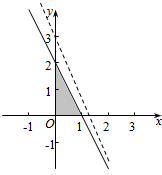 解:满足不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{2x+y≤2}\end{array}\right.$的平面区域如右图所示,
解:满足不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{2x+y≤2}\end{array}\right.$的平面区域如右图所示,
由于对任意的实数x、y,不等式ax+y≤3恒成立,
根据图形,可得斜率-a≥0或-a>kAB=$\frac{3-0}{0-1}$=-3,
解得:a≤3,
则实数a的取值范围是(-∞,3].
故答案为:(-∞,3].
点评 此题考查了简单线性规划,画出正确的图形是解本题的关键.

练习册系列答案
相关题目
15.函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(x≥0)}\\{f(x+1)(x<0)}\end{array}\right.$,若方程f(x)=-x+a有且只有两个不等的实数根,则实数a的取值范围为( )
| A. | (-∞,0) | B. | [0,1) | C. | (-∞,1) | D. | [0,+∞) |
9.已知集合M={0,1},集合N={x|x2+x=0},则集合M∩N=( )
| A. | 0 | B. | ∅ | C. | {0} | D. | {-1,0,1} |
13.若点A(-2,m)在正比例函数y=-$\frac{1}{2}$x的图象上,则m的值是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 1 | D. | -1 |