题目内容
已知命题P:函数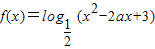 在(-∞,1]内为单调递增函数,命题Q:函数f(x)=x|x-a|+2x在R上单调递增;
在(-∞,1]内为单调递增函数,命题Q:函数f(x)=x|x-a|+2x在R上单调递增;(1)若命题Q为真,求实数a的范围;
(2)若p∨q为真,p∧q为假,求实数a的取值范围.
【答案】分析:(1)对a分类讨论:f(x)=x|x-a|+2x=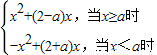 ,由命题Q:函数f(x)在R上是增函数,则
,由命题Q:函数f(x)在R上是增函数,则 解出即可.
解出即可.
(2)先化简命题P,由命题p∨q为真,p∧q为假,等价于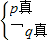 或
或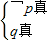 .解出即可.
.解出即可.
解答:解:(1)f(x)=x|x-a|+2x=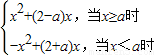 ,
,
由命题Q:函数f(x)在R上是增函数,则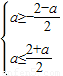 解得-2≤a≤2,
解得-2≤a≤2,
∴a的取值范围是-2≤a≤2.
(2)由已知命题P:函数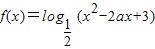 在(-∞,1]内为单调递增函数,
在(-∞,1]内为单调递增函数,
∴函数g(x)=x2-2ax+3在(-∞,1]内大于零且单调递减,
∴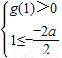 ,解得1≤a<2.
,解得1≤a<2.
∵命题p∨q为真,p∧q为假,∴等价于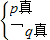 或
或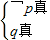 .
.
由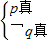 解得-2≤a<1或a=2;
解得-2≤a<1或a=2;
或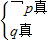 .解得a∈Φ.
.解得a∈Φ.
综上可知实数a的取值范围是[-2,1)∪{2}.
点评:本题综合考查了函数的性质和复合命题的真假,掌握以上知识及分类讨论的思想方法是解决问题的关键.
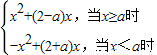 ,由命题Q:函数f(x)在R上是增函数,则
,由命题Q:函数f(x)在R上是增函数,则 解出即可.
解出即可.(2)先化简命题P,由命题p∨q为真,p∧q为假,等价于
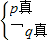 或
或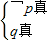 .解出即可.
.解出即可.解答:解:(1)f(x)=x|x-a|+2x=
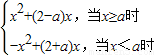 ,
,由命题Q:函数f(x)在R上是增函数,则
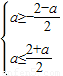 解得-2≤a≤2,
解得-2≤a≤2,∴a的取值范围是-2≤a≤2.
(2)由已知命题P:函数
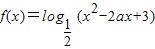 在(-∞,1]内为单调递增函数,
在(-∞,1]内为单调递增函数,∴函数g(x)=x2-2ax+3在(-∞,1]内大于零且单调递减,
∴
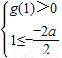 ,解得1≤a<2.
,解得1≤a<2.∵命题p∨q为真,p∧q为假,∴等价于
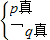 或
或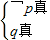 .
.由
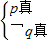 解得-2≤a<1或a=2;
解得-2≤a<1或a=2;或
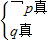 .解得a∈Φ.
.解得a∈Φ.综上可知实数a的取值范围是[-2,1)∪{2}.
点评:本题综合考查了函数的性质和复合命题的真假,掌握以上知识及分类讨论的思想方法是解决问题的关键.

练习册系列答案
相关题目
 1常数,求函数
1常数,求函数 定义
定义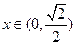 上单调递增;命题Q:不等式
上单调递增;命题Q:不等式 对任意实数
对任意实数 恒成立;若
恒成立;若 是真命题,求实数
是真命题,求实数 的取值范
的取值范 1常数,求函数
1常数,求函数 定义
定义 上单调递增;命题Q:不等式
上单调递增;命题Q:不等式 对任意实数
对任意实数 恒成立;若
恒成立;若 是真命题,求实数
是真命题,求实数 的取值范
的取值范