题目内容
（12分）已知命题P：函数
在区间[－1，3]上的最小值等于2；命题Q：不等式
对任意
恒成立。如果上述两个命题中有且仅有一个真命题，试求实数m的取值范围。
解析：若命题P为真，由
，对称轴x＝2m
当2m
1即m
时，
在[－1,3]上为增函数
即4m2+4m+1=0
得
当
即
时
符合
当2m＞3即m＞
时，在[－1,3]上为减函数
即（2m－3）2＝0
不符合
综上可知，若P为真，则
…………………（4分）
又若命题Q为真，由x+|x－m|=
∴要不等式x+|x－m|＞1对任意
恒成立，则m＞1
∴若Q为真，则则m＞1………………………………（7分）
而上述两个命题中有且仅有一个真命题
∴①当P真Q假，有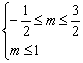
得
…（9分）
②当P假Q真，有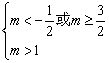
得
…（11分）
综合①②知，满足条件的实数m的取值范围是
……………………………………（12分） 
练习册系列答案
阅读快车系列答案
相关题目