题目内容
数列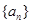 的前n项和为
的前n项和为 ,
,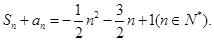
(I)证明:数列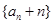 是等比数列;
是等比数列;
(Ⅱ)若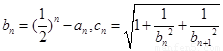 ,数列
,数列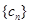 的前n项和为
的前n项和为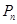 ,求不超过
,求不超过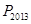 的最大整数的值.
的最大整数的值.
【答案】
(1)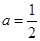 (2)定义域为
(2)定义域为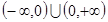 (3) 在
(3) 在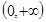 上单调递增,
上单调递增, 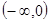 上单调递增
上单调递增
【解析】
试题分析:(1)因为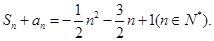 看到
看到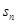 我们容易想到利用
我们容易想到利用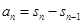 求解.但要注意当
求解.但要注意当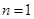 的时候.(2)
的时候.(2)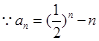
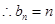
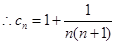 ,再利用裂项相消求和解不等式求解.
,再利用裂项相消求和解不等式求解.
试题解析:(Ⅰ) 因为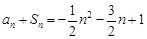 ,
,
所以① 当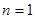 时,
时, ,则
,则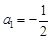 .
.
② 当 时,
时,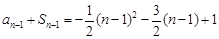 .
.
所以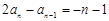 ,即
,即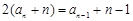 ,
,
而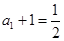 ,所以数列
,所以数列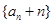 是首项为
是首项为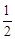 ,公比为
,公比为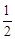 的等比数列,
的等比数列,
所以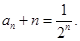 6分
6分
(Ⅱ)由(Ⅰ)知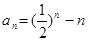 ,
, 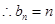 .
.
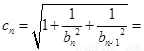
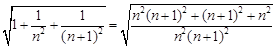
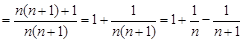 , 所以
, 所以
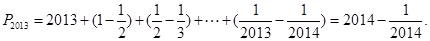
故不超过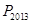 的最大整数为
的最大整数为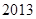 . 12分
. 12分
考点:数列求通项、数列求和

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
