题目内容
已知:有穷数列{an}共有2k项(整数k≥2 ),a1=2,设该数列的前n项和为Sn且满足Sn+1=aSn+2(n=1,2,…,2k-1),a>1.(1)求{an}的通项公式.
(2)设bn=log2an,求{bn}的前n项和Tn.
(3)设cn=
| Tn |
| n |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 36 |
| 11 |
分析:(1)由Sn+1=aSn+2(n=1,2,2k-1),知Sn=aSn-1+2(n=2,3,k),由此得an+1=a•an,从而能求出{an}的通项公式.
(2)由bn-bn-1=log2an-log2an-1=log2an-1log2
=log2a(n=2,3,2k),知{bn}是以b1=1为首项,以log2a(a>1)为公差的等差数列,由此能求出Tn.
(3)cn=
=1+
=1+
(n=1,2,2k),当cn≤
时,n≤k+
,n为正整数,知n≤k时,cn<
.当n≥k+1时,11k2-72k+3≥0,由此解得满足条件的k的最小值为6.
(2)由bn-bn-1=log2an-log2an-1=log2an-1log2
| an |
| an-1 |
(3)cn=
| Tn |
| n |
| (n-1)logx2kx-1 |
| 2 |
| n-1 |
| 2k-1 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:(1)由Sn+1=aSn+2(n=1,2,2k-1)(1)
Sn=aSn-1+2(n=2,3,k)(2)
(1)-(2)得an+1=a•an(n=2,3,2k-1)
由(1)式S2=aS1+2,a1+a2=aS1+2
解得a2=2a,因为
=a
所以{an}是以2为首项,a为公比的等比数列,an=2•an-1(n=1,2,2k)
(2)∵bn-bn-1=log2an-log2an-1=log2an-1log2
=log2a(n=2,3,2k)
∴{bn}是以b1=1为首项,以log2a(a>1)为公差的等差数列
∴Tn=
=
=n+
(a>1,n=1,2,2k)
(3)cn=
=1+
=1+
(n=1,2,2k)
当cn≤
时,n≤k+
,n为正整数,知n≤k时,cn<
当n≥k+1时,cn>
|c1-
|+|c2-
|+…|c2k-1-
|+|c2k-
|
=(
-c1)+(
-c2)++(
-ck)+(ck+1-
)++(c2k-
)
=(ck+1+ck+2++c2k)-(c1+c2++ck)
=
{[k+(k+1)++(2k-1)]+2k}-
{[1+2++(k-1)]+k}
=
[
-
]
=
≥
即11k2-72k+3≥0,(11k-6)(k-6)≥0解得k≥6或k≤
所以满足条件的k的最小值为6.
Sn=aSn-1+2(n=2,3,k)(2)
(1)-(2)得an+1=a•an(n=2,3,2k-1)
由(1)式S2=aS1+2,a1+a2=aS1+2
解得a2=2a,因为
| a2 |
| a1 |
所以{an}是以2为首项,a为公比的等比数列,an=2•an-1(n=1,2,2k)
(2)∵bn-bn-1=log2an-log2an-1=log2an-1log2
| an |
| an-1 |
∴{bn}是以b1=1为首项,以log2a(a>1)为公差的等差数列
∴Tn=
| (1+logx2•an-1)n |
| 2 |
| (2+(n-1)logxa)n |
| 2 |
=n+
| n(n-1)logxa |
| 2 |
(3)cn=
| Tn |
| n |
| (n-1)logx2kx-1 |
| 2 |
| n-1 |
| 2k-1 |
当cn≤
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当n≥k+1时,cn>
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
=(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
=(ck+1+ck+2++c2k)-(c1+c2++ck)
=
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
=
| 1 |
| 2k-1 |
| k(3k-1) |
| 2 |
| k(k-1) |
| 2 |
=
| k-1 |
| 2k-1 |
| 36 |
| 11 |
即11k2-72k+3≥0,(11k-6)(k-6)≥0解得k≥6或k≤
| 36 |
| 11 |
所以满足条件的k的最小值为6.
点评:本题考查数列的性质和应用,解题时要注意公式的合理运用.

练习册系列答案
相关题目
 ,若a=2
,若a=2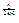 ,求满足不等式
,求满足不等式 +
+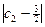 +…+
+…+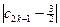 +
+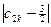 ≥
≥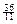 时k的最小值.
时k的最小值.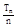 ,若a=2
,若a=2 ,求满足不等式
,求满足不等式 +
+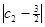 +…+
+…+ +
+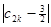 ≥
≥ 时k的最小值.
时k的最小值. ,若
,若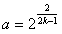 ,求满足不等式
,求满足不等式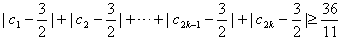 时k的最小值。
时k的最小值。