题目内容
(10分)(本题192班必做题,其他班不做)
已知二次函数f(x)=ax2+bx+c,若f(x)+f(x+1)=2x2-2x+13
(1)求函数f(x)的解析式;
(2)画该函数的图象;
(3)当x∈[t,5]时,求函数f(x)的最大值.
已知二次函数f(x)=ax2+bx+c,若f(x)+f(x+1)=2x2-2x+13
(1)求函数f(x)的解析式;
(2)画该函数的图象;
(3)当x∈[t,5]时,求函数f(x)的最大值.
解:(1)f(x)+f(x+1)=ax2+bx+c+a(x+1)2+b(x+1)+c
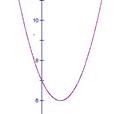
=2ax2+(2a+2b)x+a+b+2c ………………………………2分
∵f(x)+f(x+1)=2x2-2x+13
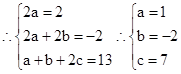 ∴f(x)=x2-2x+7……………… 6分
∴f(x)=x2-2x+7……………… 6分
(2)
………………………8分
(3)当-3≤t≤5时,函数f(x)的最大值为22
当t<-3时,函数f(x)的最大值为t2-2t+7 ……………………… 12分

=2ax2+(2a+2b)x+a+b+2c ………………………………2分
∵f(x)+f(x+1)=2x2-2x+13
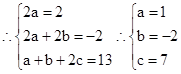 ∴f(x)=x2-2x+7……………… 6分
∴f(x)=x2-2x+7……………… 6分(2)
………………………8分
(3)当-3≤t≤5时,函数f(x)的最大值为22
当t<-3时,函数f(x)的最大值为t2-2t+7 ……………………… 12分
略

练习册系列答案
相关题目
 +2x+3, x
+2x+3, x ,x
,x
 R,x
R,x x
x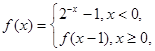 则满足
则满足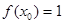 的实数
的实数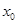 的集合是 .
的集合是 .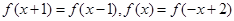 ,方程
,方程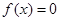 在
在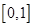 内有且只有一个根
内有且只有一个根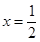 ,则
,则 内根的个数为 ( )
内根的个数为 ( )



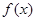 对任意实数
对任意实数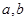 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当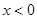 时,
时, .
.  ;
; 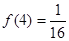 时,解不等式
时,解不等式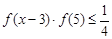
 ,若
,若  ,则
,则
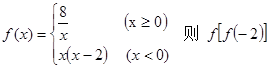 =
= 
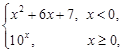 则
则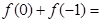 ( ▲ )
( ▲ )

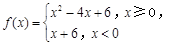 ,则
,则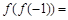 _____________.
_____________.