题目内容
已知函数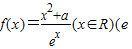 是自然对数的底数,e≈2.71)
是自然对数的底数,e≈2.71)(1)当a=-15时,求f(x)的单调区间;
(2)若f(x)在区间
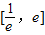 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;(3)证明
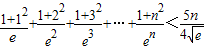 对一切n∈N*恒成立.
对一切n∈N*恒成立.
【答案】分析:(1)求导函数,由f′(x)>0,可得函数的单调增区间;由f′(x)<0,可得函数的单调减区间
(2)求导函数,根据f(x)在区间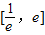 上是增函数,转化为(x-1)2≤1-a在区间
上是增函数,转化为(x-1)2≤1-a在区间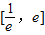 上恒成立,求出x∈
上恒成立,求出x∈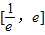 时,(x-1)2的最大值,即可求得实数a的取值范围;
时,(x-1)2的最大值,即可求得实数a的取值范围;
(3)令a=1,则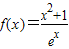 ,可得f(x)在(-∞,+∞)上为减函数,对于任意k∈N*,都有
,可得f(x)在(-∞,+∞)上为减函数,对于任意k∈N*,都有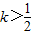 ,故有
,故有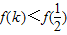 ,从而可证结论.
,从而可证结论.
解答:(1)解:当a=-15时,f(x)=(x2-15)e-x
求导函数,可得f′(x)=-(x-5)(x+3)e-x
令f′(x)=0得x=-3或x=5
由f′(x)>0,可得-3<x<5;由f′(x)<0,可得x<-3或x>5
∴函数的单调增区间为(-3,5),减区间为(-∞,-3),(5,+∞)
(2)解:f′(x)=-(x2-2x+a)e-x
∵f(x)在区间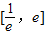 上是增函数,∴f′(x)=-(x2-2x+a)e-x≥0在区间
上是增函数,∴f′(x)=-(x2-2x+a)e-x≥0在区间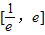 上恒成立
上恒成立
∴(x-1)2≤1-a在区间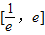 上恒成立
上恒成立
当x∈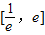 时,(x-1)2的最大值为(e-1)2,∴(e-1)2≤1-a
时,(x-1)2的最大值为(e-1)2,∴(e-1)2≤1-a
∴a≤2e-e2
∴实数a的取值范围为(-∞,2e-e2];
(3)证明:令a=1,则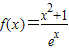 ,
,
∴f′(x)=-(x-1)2e-x≤0
∴f(x)在(-∞,+∞)上为减函数,对于任意k∈N*,都有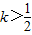 ,故有
,故有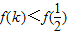
即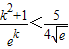
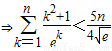
即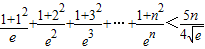 . …(12分)
. …(12分)
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查不等式的证明.恒成立问题通常利用分离参数法,利用函数的最值求解.
(2)求导函数,根据f(x)在区间
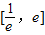 上是增函数,转化为(x-1)2≤1-a在区间
上是增函数,转化为(x-1)2≤1-a在区间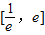 上恒成立,求出x∈
上恒成立,求出x∈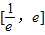 时,(x-1)2的最大值,即可求得实数a的取值范围;
时,(x-1)2的最大值,即可求得实数a的取值范围;(3)令a=1,则
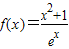 ,可得f(x)在(-∞,+∞)上为减函数,对于任意k∈N*,都有
,可得f(x)在(-∞,+∞)上为减函数,对于任意k∈N*,都有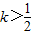 ,故有
,故有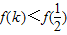 ,从而可证结论.
,从而可证结论.解答:(1)解:当a=-15时,f(x)=(x2-15)e-x
求导函数,可得f′(x)=-(x-5)(x+3)e-x
令f′(x)=0得x=-3或x=5
由f′(x)>0,可得-3<x<5;由f′(x)<0,可得x<-3或x>5
∴函数的单调增区间为(-3,5),减区间为(-∞,-3),(5,+∞)
(2)解:f′(x)=-(x2-2x+a)e-x
∵f(x)在区间
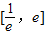 上是增函数,∴f′(x)=-(x2-2x+a)e-x≥0在区间
上是增函数,∴f′(x)=-(x2-2x+a)e-x≥0在区间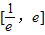 上恒成立
上恒成立∴(x-1)2≤1-a在区间
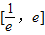 上恒成立
上恒成立当x∈
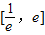 时,(x-1)2的最大值为(e-1)2,∴(e-1)2≤1-a
时,(x-1)2的最大值为(e-1)2,∴(e-1)2≤1-a∴a≤2e-e2
∴实数a的取值范围为(-∞,2e-e2];
(3)证明:令a=1,则
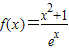 ,
,∴f′(x)=-(x-1)2e-x≤0
∴f(x)在(-∞,+∞)上为减函数,对于任意k∈N*,都有
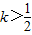 ,故有
,故有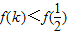
即
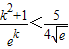
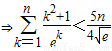
即
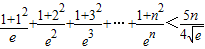 . …(12分)
. …(12分)点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查不等式的证明.恒成立问题通常利用分离参数法,利用函数的最值求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
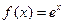 (
(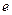 是自然对数的底数,
是自然对数的底数,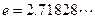 ).
).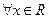 ,不等式
,不等式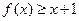 恒成立;
恒成立;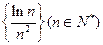 的前
的前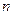 项和为
项和为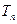 ,求证:
,求证: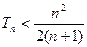 .
. (
( 是自然对数的底数).
是自然对数的底数). ,不等式
,不等式 恒成立;
恒成立; 的前
的前 项和为
项和为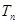 ,求证:
,求证: .
. 是自然对数的底)
是自然对数的底) 的单调区间;
的单调区间; 时,若方程
时,若方程 在区间
在区间 上有两个不同的实根,求证:
上有两个不同的实根,求证: 。
。 (
( 是自然对数的底数,
是自然对数的底数, ).
). ,不等式
,不等式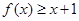 恒成立;
恒成立; 的前
的前 项和为
项和为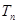 ,求证:
,求证: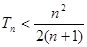 .
.