题目内容
(本题10分)
已知函数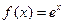 (
(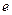 是自然对数的底数,
是自然对数的底数,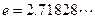 ).
).
(I)证明:对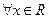 ,不等式
,不等式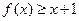 恒成立;
恒成立;
(II)数列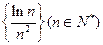 的前
的前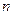 项和为
项和为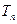 ,求证:
,求证: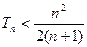 .
.
解:(I)设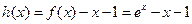
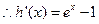 ,当
,当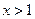 时,
时,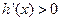 函数
函数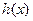 单调递增;
单调递增;
当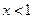 时,
时,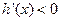 ,函数
,函数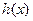 单调递减. 当
单调递减. 当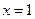 时,
时,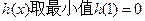 .
.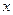
(-∞,1) 1 (1,+∞) 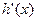
- 0 + 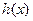
递减 极小值 递增 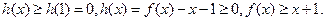
(II)由(I)可知,对任意的实数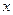 ,不等式
,不等式 恒成立,设
恒成立,设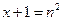
所以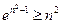 ,
,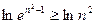 ,即
,即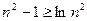 ,
,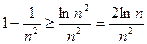 ,
,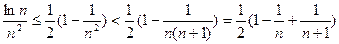
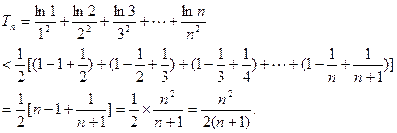
解析

练习册系列答案
相关题目
题目内容
(本题10分)
已知函数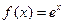 (
(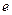 是自然对数的底数,
是自然对数的底数,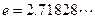 ).
).
(I)证明:对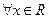 ,不等式
,不等式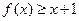 恒成立;
恒成立;
(II)数列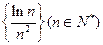 的前
的前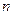 项和为
项和为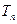 ,求证:
,求证: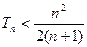 .
.
解:(I)设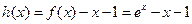
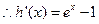 ,当
,当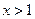 时,
时,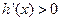 函数
函数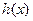 单调递增;
单调递增;
当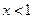 时,
时,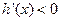 ,函数
,函数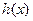 单调递减. 当
单调递减. 当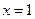 时,
时,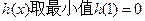 .
.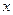
(-∞,1) 1 (1,+∞) 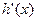
- 0 + 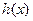
递减 极小值 递增 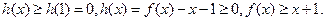
(II)由(I)可知,对任意的实数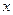 ,不等式
,不等式 恒成立,设
恒成立,设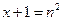
所以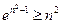 ,
,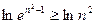 ,即
,即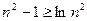 ,
,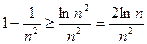 ,
,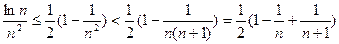
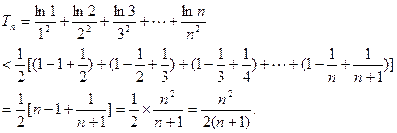
解析
