题目内容
5.已知在△ABC中,若sinA+cosA=$\frac{1}{5}$,求sinAcosA+sinA-cosA的值.分析 把已知等式两边平方,利用完全平方公式化简,整理求出sinAcosA的值,再利用完全平方公式及同角三角函数间基本关系化简,即可求出sinA-cosA的值.
解答 解:在△ABC中,sinA+cosA=$\frac{1}{5}$,
两边平方得:(sinA+cosA)2=1+2sinAcosA=$\frac{1}{25}$,即2sinAcosA=-$\frac{24}{25}$,
∴sinAcosA=-$\frac{12}{25}$,
∴cosA<0,sinA>0,即sinA-cosA>0,
∴(sinA-cosA)2=1-2sinAcosA=$\frac{49}{25}$,即sinA-cosA=$\frac{7}{5}$,
则原式=-$\frac{12}{25}$+$\frac{7}{5}$=$\frac{13}{25}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
16. 某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )
某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )
 某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )
某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )| A. | 1 | B. | 2 | C. | $\frac{7}{4}$ | D. | $\frac{9}{4}$ |
14.复数$\frac{1}{2-i}$的虚部为( )
| A. | $\frac{1}{5}i$ | B. | $\frac{1}{5}$ | C. | $\frac{\sqrt{5}}{5}i$ | D. | $\frac{\sqrt{5}}{5}$ |
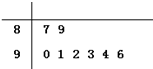 某校高二年级8个班参加合唱比赛的得分如面茎叶图所示,则这组数据的中位数和平均数为91.5和91.5.
某校高二年级8个班参加合唱比赛的得分如面茎叶图所示,则这组数据的中位数和平均数为91.5和91.5.