题目内容
(2013•顺义区一模)在平面直角坐标系xoy中,设抛物线y2=4x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如果直线AF的倾斜角为120°,那么|PF|=
4
4
.分析:利用抛物线的定义,|PF|=|PA|,设F在l上的射影为F′,依题意,可求得|FF′|,|AF′|,从而可求得点P的纵坐标,代入抛物线方程可求得点P的横坐标,从而可求得|PA|.
解答: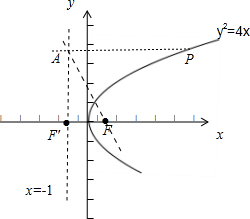 解:∵抛物线y2=4x的焦点为F,准线为l,P为抛物线上一点,
解:∵抛物线y2=4x的焦点为F,准线为l,P为抛物线上一点,
∴|PF|=|PA|,F(1,0),准线l的方程为:x=-1;
设F在l上的射影为F′,又PA⊥l,
依题意,∠AFF′=60°,|FF′|=2,
∴|AF′|=2
,PA∥x轴,
∴点P的纵坐标为2
,设点P的横坐标为x0,则(2
)2=4x0,
∴x0=3,
∴|PF|=|PA|=x0-(-1)=3-(-1)=4.
故答案为:4.
 解:∵抛物线y2=4x的焦点为F,准线为l,P为抛物线上一点,
解:∵抛物线y2=4x的焦点为F,准线为l,P为抛物线上一点,∴|PF|=|PA|,F(1,0),准线l的方程为:x=-1;
设F在l上的射影为F′,又PA⊥l,
依题意,∠AFF′=60°,|FF′|=2,
∴|AF′|=2
| 3 |
∴点P的纵坐标为2
| 3 |
| 3 |
∴x0=3,
∴|PF|=|PA|=x0-(-1)=3-(-1)=4.
故答案为:4.
点评:本题考查抛物线的简单性质,考查转化思想,考查解三角形的能力,属于中档题.

练习册系列答案
相关题目