题目内容
设f-1(x)是函数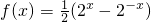 的反函数,则使f-1(x)>1成立的x的取值范围为
的反函数,则使f-1(x)>1成立的x的取值范围为
- A.(
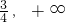 )
) - B.(
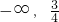 )
) - C.(
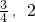 )
) - D.[2,+∞)
A
分析:首先由函数f(x)= (2x-2-x)求其反函数,要用到解指数方程,整体换元的思想,将2x看作整体解出,然后由f-1(x)>1构建不等式解出即可.
(2x-2-x)求其反函数,要用到解指数方程,整体换元的思想,将2x看作整体解出,然后由f-1(x)>1构建不等式解出即可.
解答:由题意设y= (2x-2-x)整理化简得22x-2y2x-1=0,
(2x-2-x)整理化简得22x-2y2x-1=0,
解得: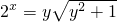
∵2x>0,∴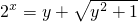 ,
,
∴x=log2(y+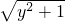 )
)
∴f-1(x)=log2(x+ )
)
由使f-1(x)>1得log2(x+ )>1
)>1
∵2>1,∴x+ >2
>2
由此解得:x>
故选A.
点评:本题考查反函数的概念、求反函数的方法、解指数方程、解不等式等知识点,有一定的综合性,属于中档题.
分析:首先由函数f(x)=
 (2x-2-x)求其反函数,要用到解指数方程,整体换元的思想,将2x看作整体解出,然后由f-1(x)>1构建不等式解出即可.
(2x-2-x)求其反函数,要用到解指数方程,整体换元的思想,将2x看作整体解出,然后由f-1(x)>1构建不等式解出即可.解答:由题意设y=
 (2x-2-x)整理化简得22x-2y2x-1=0,
(2x-2-x)整理化简得22x-2y2x-1=0,解得:
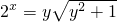
∵2x>0,∴
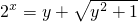 ,
,∴x=log2(y+
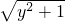 )
)∴f-1(x)=log2(x+
 )
)由使f-1(x)>1得log2(x+
 )>1
)>1∵2>1,∴x+
 >2
>2由此解得:x>

故选A.
点评:本题考查反函数的概念、求反函数的方法、解指数方程、解不等式等知识点,有一定的综合性,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
设f-1(x)是函数f(x)=2x-(
)x+x的反函数,则使f-1(x)>1成立的x的取值范围是( )
| 1 |
| 3 |
A、(-∞,
| ||
B、(
| ||
C、(0,
| ||
D、(1,
|