题目内容
(本小题满分12分)
已知函数f(x)=2sinωx·cos(ωx+)+(ω>0)的最小正周期为4π.
(1)求正实数ω的值;
(2)在△ABC中,内角A、B、C的对边分别为a、b、c,且满足2bcosA=acosC+ccosA,求f(A)的值.
已知函数f(x)=2sinωx·cos(ωx+)+(ω>0)的最小正周期为4π.
(1)求正实数ω的值;
(2)在△ABC中,内角A、B、C的对边分别为a、b、c,且满足2bcosA=acosC+ccosA,求f(A)的值.
(1)ω=.
(2)f(A)=sin(×+)=sin=.
(2)f(A)=sin(×+)=sin=.
解:(1)∵f(x)=2sinωx(cosωx·cos-sinωx·sin)+(2分)
=sinωxcosωx-sin2ωx+
=sin2ωx-(1-cos2ωx)+=sin(2ωx+).(5分)
又f(x)的最小正周期T==4π,则ω=.(6分)
(2)由2bcosA=acosC+ccosA及正弦定理可得2sinBcosA=sinAcosC+sinCcosA=sin(A+C).
又A+B+C=π,则2sinBcosA=sinB.(8分)
而sinB≠0,则cosA=.又A∈(0,π),故A=.(10分)
由(1)f(x)=sin(+),从而f(A)=sin(×+)=sin=.(12分)
=sinωxcosωx-sin2ωx+
=sin2ωx-(1-cos2ωx)+=sin(2ωx+).(5分)
又f(x)的最小正周期T==4π,则ω=.(6分)
(2)由2bcosA=acosC+ccosA及正弦定理可得2sinBcosA=sinAcosC+sinCcosA=sin(A+C).
又A+B+C=π,则2sinBcosA=sinB.(8分)
而sinB≠0,则cosA=.又A∈(0,π),故A=.(10分)
由(1)f(x)=sin(+),从而f(A)=sin(×+)=sin=.(12分)

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
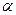 ,
,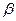 满足:
满足: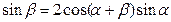 ,记
,记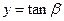 ,
,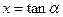 ,
,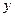 关于
关于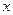 的函数解析式
的函数解析式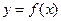 及定义域;
及定义域;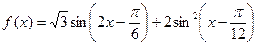 (
(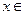 R).
R).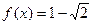 且
且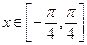 ,求x;(Ⅱ)求函数
,求x;(Ⅱ)求函数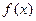 的单调递增区间.
的单调递增区间.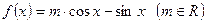
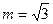 时,求函数
时,求函数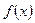 的单调递增区间;
的单调递增区间;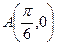 ,
,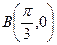 ,存在函数
,存在函数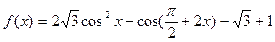
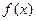 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;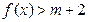 在
在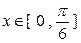 上恒成立,求实数
上恒成立,求实数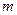 的取值范围.
的取值范围.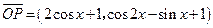 ,
,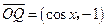 ,
,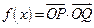
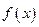 最小正周期;
最小正周期;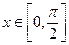 ,求函数
,求函数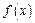 的最大值及取得最大值时的
的最大值及取得最大值时的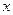 ;
;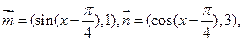
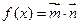 。
。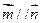 ,求
,求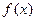 ;
;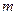 (
(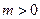 )个单位长度,再向下平移3个单位后图像对应的函数
)个单位长度,再向下平移3个单位后图像对应的函数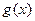 是奇函数,求
是奇函数,求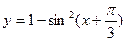 的最小正周期是 。
的最小正周期是 。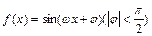 的最小正周期为
的最小正周期为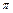 ,且其图象向左平移
,且其图象向左平移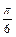 个单位后得到的函数为奇函数,则函数
个单位后得到的函数为奇函数,则函数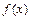 的图象( )
的图象( )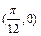 对称
对称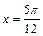 对称
对称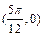 对称
对称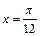 对称
对称