题目内容
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
|
分数段(分) |
[50,70) |
[70,90) |
[90,110) |
[110,130) |
[130,150) |
总计 |
|
频数 |
|
|
|
b |
|
|
|
频率 |
a |
0.25 |
|
|
|
|

(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格):
(2)从成绩大于等于110分的学生中随机选两人,求这两人成绩的平均分不小于130分的概率.
(1)a=0.1,b=3;4;65%.(2)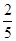 .
.
【解析】
试题分析:(1)由[50,70)范围的频数,计算出该范围内的频率a,首先计算出[70,90)范围内的频数,然后得出[80,90),即可求出[90,100)范围内的学生人数,计算出[90,100)范围内的学生人数,然后除以20就是及格率.(2)写出总的基本事件数,在找到所求事件数,根据随机事件的概率公式求解即可.
试题解析:(1)由茎叶图可知分数在[50,70)范围内的有2人,在[110,130) 范围内的有3人,
∴a=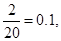 b=3;分数在[70,90)内的人数20×0.25=5,结合茎叶图可得分数在[70,80)内的人数为2,所以分数在[90,100)范围内的学生人数为4,故数学成绩及格的学生为13人,所以估计这次考试全校学生数学成绩的及格率为
b=3;分数在[70,90)内的人数20×0.25=5,结合茎叶图可得分数在[70,80)内的人数为2,所以分数在[90,100)范围内的学生人数为4,故数学成绩及格的学生为13人,所以估计这次考试全校学生数学成绩的及格率为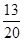 ×100%=65%.
×100%=65%.
(2)设A表示事件“从成绩大于等于110分的学生中随机选两人,其平均成绩大于等于130分”,由茎叶图可知成绩大于等于110分的学生有5人,记着5人分别为a,b,c,d,e,则选取学生的所有可能结果为:
(a,b),(a,c),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e),
基本事件为10,事件A包含的结果有:(118,142),(128,136),(128,142)(136,142),共4种情况,
所以P(A)=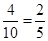
考点:1.茎叶图的含义以及频率和频数的计算;2.随机事件的概率.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案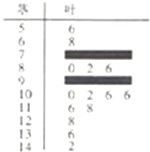 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表: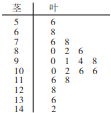 某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如下:
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如下: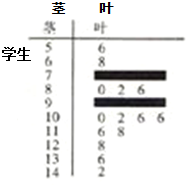 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表: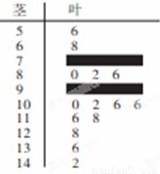

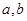 的值及分数在
的值及分数在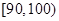 范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在
范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在 范围为及格);
范围为及格);