题目内容
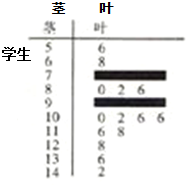 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150] | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
(2)从成绩大于等于110分的学生中随机选两人,求这两人成绩的平均分不小于130分的概率.
分析:(1)结合频率分布表与茎叶图给出的数据,先求a、b的值,再根据频率和为1,求分数在[90,110)范围内的学生数,从而求出分数分别在[90,100)和[70,90)的人数,计算及格率;
(2)由茎叶图可知成绩大于等于110分的学生有5人,从中选取2人共有
=10种方法;求出符合条件的方法数,利用古典概型概率公式计算.
(2)由茎叶图可知成绩大于等于110分的学生有5人,从中选取2人共有
| C | 2 5 |
解答:解:(1)由茎叶图可知分数在[50,70)范围内的有2人,在[110,130)范围内有3人,
∴a=
=0.1,b=3,
又分数在[110,150]范围内的频率为
=0.25,所以分数在[90,110)范围内的频率为1-0.1-0.25-0.25=0.4,
所以分数在[90,110)范围内的学生人数为20×0.4=8,
由题中的茎叶图可知分数在[100,110)范围内的学生人数为4,所以分数在[90,100)范围内的学生人数为4.
从题中的频率分布表可知分数在[70,90)范围内的频率为0.25,所以分数在[70,90)范围内的学生人数为20×0.25=5,所以数学成绩及格的学生为13人,
所以以估计这次考试全校学生数学成绩的及格率为
×100%=65%
(2)由茎叶图可知成绩大于等于110分的学生有5人,记这5人的成绩分别为116,118,128,136,142.
从中选取2人共有
=10种方法;
选取的两人,成绩的平均分不小于130分有(142,136);(142,128);(142,118);(136,128),4选法,
∴两人成绩的平均分不小于130分的概率为
=
.
∴a=
| 2 |
| 20 |
又分数在[110,150]范围内的频率为
| 5 |
| 20 |
所以分数在[90,110)范围内的学生人数为20×0.4=8,
由题中的茎叶图可知分数在[100,110)范围内的学生人数为4,所以分数在[90,100)范围内的学生人数为4.
从题中的频率分布表可知分数在[70,90)范围内的频率为0.25,所以分数在[70,90)范围内的学生人数为20×0.25=5,所以数学成绩及格的学生为13人,
所以以估计这次考试全校学生数学成绩的及格率为
| 13 |
| 20 |
(2)由茎叶图可知成绩大于等于110分的学生有5人,记这5人的成绩分别为116,118,128,136,142.
从中选取2人共有
| C | 2 5 |
选取的两人,成绩的平均分不小于130分有(142,136);(142,128);(142,118);(136,128),4选法,
∴两人成绩的平均分不小于130分的概率为
| 4 |
| 10 |
| 2 |
| 5 |
点评:本题考查了茎叶图,考查了古典概型的概率计算,考查了学生搜集信息,处理数据的能力,解答本题的关键是读懂茎叶图.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
|
分数段(分) |
[50,70) |
[70,90) |
[90,110) |
[110,130) |
[130,150) |
总计 |
|
频数 |
|
|
|
b |
|
|
|
频率 |
a |
0.25 |
|
|
|
|

(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格):
(2)从成绩大于等于110分的学生中随机选两人,求这两人成绩的平均分不小于130分的概率.
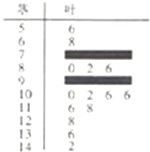 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表: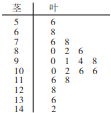 某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如下:
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如下: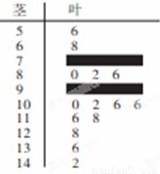

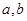 的值及分数在
的值及分数在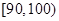 范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在
范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在 范围为及格);
范围为及格);