题目内容
【题目】函数![]() 满足
满足![]() ,
,![]() ,当
,当![]() ,
,![]() 时,
时,![]() ,(过点
,(过点![]() 且斜率为
且斜率为![]() 的直线与
的直线与![]() 在区间
在区间![]() ,
,![]() 上的图象恰好有3个交点,则
上的图象恰好有3个交点,则![]() 的取值范围为__.
的取值范围为__.
【答案】![]()
【解析】
根据函数的奇偶性及函数的图象的对称性,可求出函数在![]() ,
,![]() 上的解析式,作出函数图象,由数形结合可知直线
上的解析式,作出函数图象,由数形结合可知直线![]() 的斜率满足
的斜率满足![]() 时,直线与函数有3个交点,利用导数及斜率公式可求出
时,直线与函数有3个交点,利用导数及斜率公式可求出![]() ,即可求解.
,即可求解.
由![]() ,
,![]() 时,
时,![]() ,以及
,以及![]() 可知,
可知,
当![]() 时,
时,![]() ,
,
又由![]() ,可知函数
,可知函数![]() 图象关于直线
图象关于直线![]() 对称,
对称,
故当![]() 时,
时,![]() ,
,
则![]() ,
,![]() ,
,
即![]() 时,
时,![]() ,
,
同理可知,当![]() 时,
时,![]() ,
,
又直线恒过点![]() ,
,
故其方程为![]() ,即
,即![]() ,
,
做出函数![]() 当
当![]() 时的函数图象和
时的函数图象和![]() ,
,
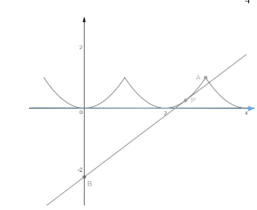
由图象可知,适合题意的![]() 的范围是
的范围是![]() ,
,
设直线和函数在![]() ,
,![]() 上相切于点
上相切于点![]() ,
,![]() ,
,
则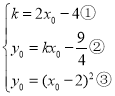
将②代入③,得到![]() ④
④
再将①代入④得到,![]()
解得![]() ,故
,故![]() ,舍去负值.
,舍去负值.
将![]() 代入①,得到
代入①,得到![]() ,
,
又由题可知点![]() ,代入直线
,代入直线![]() ,
,
得到![]() ,
,
故适合题意的![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目