题目内容
已知双曲线C1和椭圆C2有相同的焦点F1(-c,0),F2(c,0)(c>0),两曲线在第一象限内的交点为P,椭圆C2与y轴负方向交点为B,且P、F2、B三点共线,F2与![]() 的比为1:2,又直线PB与双曲线C1的另一交点为Q(如图),若|F2Q|=
的比为1:2,又直线PB与双曲线C1的另一交点为Q(如图),若|F2Q|=![]() ,求双曲线C1,椭圆C2的方程。
,求双曲线C1,椭圆C2的方程。

答案:
解析:
解析:
依题意,可设C2: 显然B(0,-b),由 由P∈C2,∴ ∴a2=3c2,b2=2c2, 由P∈C1有 ∴4n4+7c2n2-2c4=0 ∴(4n2-c2)(n2+2c2)=0, 即 直线PF2的方程即为y= 20x2-48cx+27c2=0∴x= ∴( 由距离公式及 ∴ 所求双曲线C1的方程是
|

练习册系列答案
相关题目

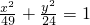 有公共的焦点,它们的离心率分别是e1和e2,且
有公共的焦点,它们的离心率分别是e1和e2,且 ,求双曲线C1的方程.
,求双曲线C1的方程. 有公共的焦点,它们的离心率分别是e1和e2,且
有公共的焦点,它们的离心率分别是e1和e2,且 ,求双曲线C1的方程.
,求双曲线C1的方程.